题目内容
已知f(x)为一次函数,且f(x)=x
f(x)dx+1.
(1)求f(x)的解析式;
(2)求直线y=f(x)与曲线y=xf(x)围成平面图形的面积.
| ∫ | 2 0 |
(1)求f(x)的解析式;
(2)求直线y=f(x)与曲线y=xf(x)围成平面图形的面积.
考点:函数解析式的求解及常用方法,定积分,定积分在求面积中的应用
专题:函数的性质及应用,导数的综合应用
分析:(1)设f(x)=kx+b(k≠0),代入f(x)=x
f(x)dx+1由系数相等求得k,b的值,则函数解析式可求;
(2)由y=xf(x)=x(-2x+1)=-2x2+x,联立
求得交点坐标,然后求函数xf(x)-f(x)的定积分可得直线y=f(x)与曲线y=xf(x)围成平面图形的面积.
| ∫ | 2 0 |
(2)由y=xf(x)=x(-2x+1)=-2x2+x,联立
|
解答:
解:(1)设f(x)=kx+b(k≠0),
代入f(x)=x
f(x)dx+1,得kx+b=x
(kx+b)dx+1,
即kx+b=x•(
kx2+bx)
+1=(2k+2b)x+1,
∴
,解得:
.
∴f(x)=-2x+1;
(2)y=xf(x)=x(-2x+1)=-2x2+x,
联立
,解得x1=
,x2=1.
∴直线y=f(x)与曲线y=xf(x)围成平面图形的面积:
S=
(-2x2+3x-1)dx=(-
x3+
x2-x)
=
.
代入f(x)=x
| ∫ | 2 0 |
| ∫ | 2 0 |
即kx+b=x•(
| 1 |
| 2 |
| | | 2 0 |
∴
|
|
∴f(x)=-2x+1;
(2)y=xf(x)=x(-2x+1)=-2x2+x,
联立
|
| 1 |
| 2 |
∴直线y=f(x)与曲线y=xf(x)围成平面图形的面积:
S=
| ∫ | 1
|
| 2 |
| 3 |
| 3 |
| 2 |
| | | 1
|
| 1 |
| 24 |
点评:本题考查了函数解析式的求解及常用方法,考查了利用微积分基本定理求曲边梯形的面积,是中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
若l、m、n是互不相同的空间直线,α、β是不重合的平面,则下列结论正确的是( )
| A、α∥β,l?α,n?β⇒l∥n |
| B、α∥β,l?α⇒l⊥β |
| C、l⊥n,m⊥n⇒l∥m |
| D、l⊥α,l∥β⇒α⊥β |
已知某地区多风,风力都在1~6级,下面是30天的统计数字,每三天为一组,共10组:342 136 556 461 336 516 225 213 112 341据此估计,该地区每三天就会出现两次4级及4级以上刮风天气的概率为( )
| A、0.12 | B、0.20 |
| C、0.28 | D、0.37 |
设f为实系数三次多项式函数﹒已知五个方程式的相异实根个数如下表所述﹕
关于f的极小值a﹐试问下列哪一个选项是正确的( )
| 方程式 | 相异实根的个数 |
| f(x)-20=0 | 1 |
| f(x)-10=0 | 3 |
| f(x)=0 | 3 |
| f(x)+10=0 | 1 |
| f(x)+20=0 | 1 |
| A、-20<a<-10 |
| B、-10<a<0 |
| C、0<a<10 |
| D、10<a<20 |
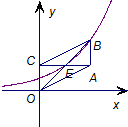 如图,面积为8的平行四边形OABC,对角线AC⊥OC,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1)的图象经过点E,B,则a=( )
如图,面积为8的平行四边形OABC,对角线AC⊥OC,AC与BO交于点E,某指数函数y=ax(a>0,且a≠1)的图象经过点E,B,则a=( )