题目内容
已知数列{bn}的前n项和为Tn，且Tn-2bn+3=0，n∈N*．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）设Cn=
，求数列{cn}的前2n+1项和P2n+1．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）设Cn=
|
考点：数列递推式,数列的求和
专题：综合题,等差数列与等比数列
分析：（Ⅰ）当n≥2时，Sn-1-2bn-1+3=0，两式相减，得数列{bn}为等比数列，即可求数列{bn}的通项公式；
（Ⅱ）确定数列{cn}的通项，利用分组求和的方法求数列{cn}的前2n+1项和P2n+1．
（Ⅱ）确定数列{cn}的通项，利用分组求和的方法求数列{cn}的前2n+1项和P2n+1．
解答：
解：（Ⅰ）∵Tn-2bn+3=0，∴当n=1时，b1=3，
当n≥2时，Sn-1-2bn-1+3=0，两式相减，得bn=2bn-1，（n≥2）
∴数列{bn}为等比数列，∴bn=3•2n-1． …（6分）
（Ⅱ）cn=
．
令an=n-1，…（8分）
故P2n+1=（a1+a3+…+a2n+1）+（b2+b4+…+b2n）=
+
…（12分）
=22n+1+n2+n-2…（14分）
当n≥2时，Sn-1-2bn-1+3=0，两式相减，得bn=2bn-1，（n≥2）
∴数列{bn}为等比数列，∴bn=3•2n-1． …（6分）
（Ⅱ）cn=
|
令an=n-1，…（8分）
故P2n+1=（a1+a3+…+a2n+1）+（b2+b4+…+b2n）=
| (0+2n)•(n+1) |
| 2 |
| 6(1-4n) |
| 1-4 |
=22n+1+n2+n-2…（14分）
点评：本题考查数列递推式，考查数列的通项与求和，确定数列{bn}为等比数列是解题的关键．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
函数f（x）=Asin（ωx+ϕ）+b的图象如图所示，则S=f（0）+f（1）+…+f（2014）等于（ ）
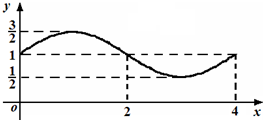
| A、0 | ||
B、
| ||
C、
| ||
D、
|
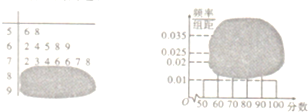某高校自主招生面试成绩的茎叶图和频率分布直方图均受到不同程度的破坏，其可见部分信息如图所示，据此解答下列问题；
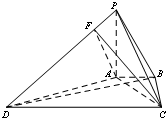如图，在四棱锥P-ABCD中，已知AB=1，BC=2，CD=4，AB∥CD，BC⊥CD，平面PAB⊥平面ABCD，PA⊥AB．
如图，PC切⊙O于点C，割线PAB经过圆心O，弦CD⊥AB于点E，已知⊙O的半径为3，PA=2，则OE=