题目内容
已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).
(1)求函数f(x)的解析式;
(2)画出函数f(x)的图象(不需列表);
(3)讨论方程f(x)-k=0的根的情况.(只需写出结果,不要解答过程)
(1)求函数f(x)的解析式;
(2)画出函数f(x)的图象(不需列表);
(3)讨论方程f(x)-k=0的根的情况.(只需写出结果,不要解答过程)
考点:函数奇偶性的性质,根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)利用函数f(x)是偶函数,及当x≥0时,f(x)=x(2-x),可以设x≤0,可得-x≥0,代入解析式化简后,由偶函数的性质即可求解;
(2)利用函数的解析式、二次函数的图象,画出函数的图象,并描出重要的点;
(3)方程f(x)=k的根的情况,利用数形结合的方法进行讨论.
(2)利用函数的解析式、二次函数的图象,画出函数的图象,并描出重要的点;
(3)方程f(x)=k的根的情况,利用数形结合的方法进行讨论.
解答:
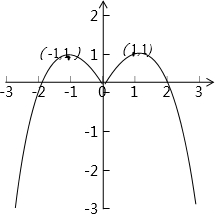 解:(1)设x≤0,则-x≥0,
解:(1)设x≤0,则-x≥0,
∵当x≥0时,f(x)=x(2-x),
∴f(-x)=-x(x+2);…1分
由f(x)是定义域为R的偶函数知:f(-x)=f(x),…2分
∴f(x)=-x(x+2),(x∈(-∞,0]);…3分
所以函数f(x)的解析式是f(x)=
.…4分
(2)函数f(x)的图象如图所示:…8分
(说明:图形形状正确,给2分;两点(-1,1),(1,1)少标示一个扣1分,共2分)
(3)由f(x)-k=0得:k=f(x),
根据函数f(x)的图象知:当k<0或k=1时,方程f(x)-k=0有两个根,…9分
当k=0时,方程f(x)-k=0有三个根,…10分
当0<k<1时,方程f(x)-k=0有四个根.…11分
当k>1时,方程f(x)-k=0没有实数根.…12分.
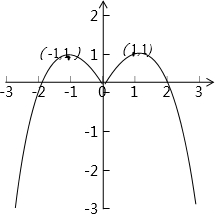 解:(1)设x≤0,则-x≥0,
解:(1)设x≤0,则-x≥0,∵当x≥0时,f(x)=x(2-x),
∴f(-x)=-x(x+2);…1分
由f(x)是定义域为R的偶函数知:f(-x)=f(x),…2分
∴f(x)=-x(x+2),(x∈(-∞,0]);…3分
所以函数f(x)的解析式是f(x)=
|
(2)函数f(x)的图象如图所示:…8分
(说明:图形形状正确,给2分;两点(-1,1),(1,1)少标示一个扣1分,共2分)
(3)由f(x)-k=0得:k=f(x),
根据函数f(x)的图象知:当k<0或k=1时,方程f(x)-k=0有两个根,…9分
当k=0时,方程f(x)-k=0有三个根,…10分
当0<k<1时,方程f(x)-k=0有四个根.…11分
当k>1时,方程f(x)-k=0没有实数根.…12分.
点评:本题主要考查偶函数的性质及其解析式的求法,二次函数的图象,利用数形结合的方法求方程解的个数,考查了数形结合思想.

练习册系列答案
相关题目
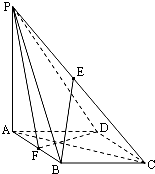 如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB中点.
如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB中点.