题目内容
已知函数f(x)=loga(x2-4x+3),求:
(1)函数f(x)的单调区间;
(2)函数f(x)的值域、定义域.
(1)函数f(x)的单调区间;
(2)函数f(x)的值域、定义域.
考点:复合函数的单调性,对数函数的定义域
专题:函数的性质及应用
分析:(1)令t=x2-4x+3=(x-2)2-1>0,求得函数的定义域,且f(x)=logat.分当a>1时、当0<a<1时两种情况,分别求出函数t在定义域内的单调区间,可得函数f(x)的单调区间.
(2)令对数的真数大于零,求得x的范围,即是函数的定义域;由于真数能取遍所有的正实数,可得f(x)的值域为R.
(2)令对数的真数大于零,求得x的范围,即是函数的定义域;由于真数能取遍所有的正实数,可得f(x)的值域为R.
解答:
解:(1)令t=x2-4x+3=(x-2)2-1>0,求得x<1,或 x>3,
故函数的定义域为(-∞,1)∪(3,+∞),且f(x)=logat.
当a>1时,由于函数t的减区间为(-∞,1),
故函数f(x)的减区间为(-∞,-1);
由于函数t的增区间为(3,-∞),故函数f(x)的增区间为(3,+∞).
当0<a<1时,由于函数t的减区间为(-∞,1),
故函数f(x)的增区间为(-∞,-1);
由于函数t的增区间为(3,-∞),故函数f(x)的减区间为(3,+∞).
(2)∵函数f(x)=loga(x2-4x+3),
∴x2-4x+3>0,求得x<1,或 x>3,
故函数的定义域为(-∞,1)∪(3,+∞).
由于t=x2-4x+3=(x-1)(x-3)能取遍所有的正实数,
故f(x)=loga(x2-4x+3)的值域为R.
故函数的定义域为(-∞,1)∪(3,+∞),且f(x)=logat.
当a>1时,由于函数t的减区间为(-∞,1),
故函数f(x)的减区间为(-∞,-1);
由于函数t的增区间为(3,-∞),故函数f(x)的增区间为(3,+∞).
当0<a<1时,由于函数t的减区间为(-∞,1),
故函数f(x)的增区间为(-∞,-1);
由于函数t的增区间为(3,-∞),故函数f(x)的减区间为(3,+∞).
(2)∵函数f(x)=loga(x2-4x+3),
∴x2-4x+3>0,求得x<1,或 x>3,
故函数的定义域为(-∞,1)∪(3,+∞).
由于t=x2-4x+3=(x-1)(x-3)能取遍所有的正实数,
故f(x)=loga(x2-4x+3)的值域为R.
点评:本题主要考查复合函数的单调性、二次函数的性质,体现了转化以及数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
某几何体三视图如图所示,则该几何几的体积等于( )


| A、2 | B、4 | C、8 | D、12 |
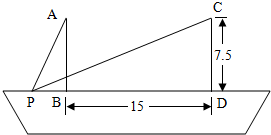 船上两根高7.5m的桅杆相距15m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧.假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.
船上两根高7.5m的桅杆相距15m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧.假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.