题目内容
17．
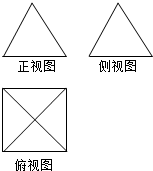若一个四梭锥的三视图如图所示，其中正视图与侧视图都是边长为2的等边三角形，则该四棱锥的四条侧棱长之和等于4$\sqrt{5}$．
分析 根据几何体的三视图，得出该几何体是底面边长为2的正四棱锥，求出高即可求出侧棱长．
解答 解：根据几何体的三视图，得；
该几何体是底面边长为2的正四棱锥，
且正四棱锥的高是$\sqrt{{2}^{2}{-（\frac{2}{2}）}^{2}}$=$\sqrt{3}$；
所以它的四条侧棱长相等，为$\sqrt{{（\sqrt{3}）}^{2}{+（\frac{2\sqrt{2}}{2}）}^{2}}$=$\sqrt{5}$；
所以，四条侧棱长之和为4$\sqrt{5}$．
故答案为：4$\sqrt{5}$．
点评 本题考查了空间几何体三视图的应用问题，也考查了空间想象能力的应用问题，是基础题目．
练习册系列答案
相关题目
7．当a＞0且a≠1时，把函数y=a-x和y=logax的图象画在同一平面直角坐标系中，可以是（ ）
| A． | ①② | B． | ①③ | C． | ②③ | D． | ③④ |
5．已知袋子中装有3个红球、2个白球、1个黑球，如果从中随机任取2个，则下列两个事件中是互斥而不对立的是（ ）
| A． | 至少有一个白球；都是白球 | B． | 至少有一个白球；至少有一个红球 | ||
| C． | 至少有一个白球；红球、黑球各一个 | D． | 恰有一个白球；白球、黑球各一个 |
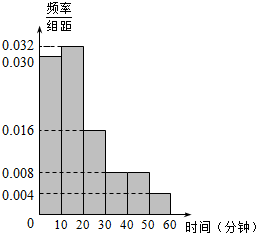某校决定为本校上学时间不少于30分钟的学生提供校车接送服务．为了解学生上学所需时间，从全校600名学生中抽取50人统计上学时间（单位：分钟），现对600人随机编号为001，002，…600．抽取50位学生上学时间均不超过60分钟，将时间按如下方式分成六组，第一组上学时间在[0，10），第二组上学时间在[10，20），…第六组上学时间在[50，60]得到各组人数的频率分布直方图．如图．
6．已知复数z1=a+bi，z2=-1+ai（a，b∈R），若|z1|＜|z2|，则（ ）
| A． | b＜-1或b＞1 | B． | -1＜b＜1 | C． | b＞1 | D． | b＞0 |