题目内容
7.在某校组织的一次篮球定点投篮测试中,规定每人最多投3次.每次投篮的结果相互独立.在M处每投进一球得3分,在N处每投进一球得2分,否则得0分.将学生得分逐次累加并用X表示,如果X的值不低于3分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1,先在M处投一球,以后都在N处投;方案2,都在N处投篮.甲同学在M处投篮的命中率为0.2,在N处投篮的命中率为0.5.(1)当甲同学选择方案1时,求甲同学测试结束后所得总分X的分布列和数学期望E(X);
(2)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
分析 (1)甲同学测试结束后所得总分X的可能值为0,2,3,4,分别求出相应的概率,由此能求出X的分布列和数学期望E(X).
(2)甲同学选择1方案通过测试的概率为P1,选择2方案通过测试的概率为P2,由已知条件求出P2>P1,从而得到甲同学选择方案2通过测试的可能性更大.
解答 解:(1)设该同学在M处投中为事件A,不中为事件$\overline{A}$,
在N处投中为事件B,不中为事件$\overline{B}$.则事件A,B相互独立,
甲同学测试结束后所得总分X的可能值为0,2,3,4.
则P(X=0)=P($\overline{A}$$\overline{B}$$\overline{B}$)=P($\overline{A}$)P($\overline{B}$)P($\overline{B}$)=0.8×0.5×0.5=0.2,
P(X=2)=P($\overline{A}$B$\overline{B}$)+P($\overline{A}$$\overline{B}$B)=P($\overline{A}$)P(B)P($\overline{B}$)+P($\overline{A}$)P($\overline{B}$)P(B)=0.8×0.5×0.5+0.8×0.5×0.5=0.4,
P(X=3)=P(A)=0.2,
P(X=4)=P($\overline{A}$BB)=P($\overline{A}$)P(B)P(B)=0.8×0.5×0.5=0.2,
∴X的分布列为:
| X | 0 | 2 | 3 | 4 |
| P | 0.2 | 0.4 | 0.2 | 0.2 |
(2)甲同学选择1方案通过测试的概率为P1,选择2方案通过测试的概率为P2,
则P1=P(X≥3)=0.2+0.2=0.4,
P2=P($\overline{B}$BB)+P(B$\overline{B}$B)+P(BB)=0.5×0.5×0.5+0.5×0.5×0.5+0.5×0.5=0.5,
∵P2>P1,∴甲同学选择方案2通过测试的可能性更大.(12分)
点评 本题考查离散型随机变量的分布列、数学期望及应用,是中档题,解题时要认真审题,注意对立事件的概率计算公式的合理运用.

练习册系列答案
相关题目
2.已知函数f(x)=log${\;}_{\frac{1}{2}}$x,x∈[$\frac{1}{4}$,$\frac{\sqrt{2}}{2}$],则f(x)的值域是( )
| A. | [$\frac{1}{2}$,2] | B. | [-$\frac{1}{2}$,2] | C. | [0,2] | D. | [0,$\frac{1}{2}$] |
12.将y=sin2x的图象水平向( )个单位后,可得到y=sin(2x+2)的图象.
| A. | 左平移2 | B. | 左平移1 | C. | 右平移2 | D. | 右平移1 |
16.在正三角形ABC中,D是BC上的点,且AB=4,BD=1,则$\overrightarrow{AB}$•$\overrightarrow{AD}$=( )
| A. | 4 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 14 |
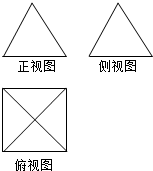 若一个四梭锥的三视图如图所示,其中正视图与侧视图都是边长为2的等边三角形,则该四棱锥的四条侧棱长之和等于4$\sqrt{5}$.
若一个四梭锥的三视图如图所示,其中正视图与侧视图都是边长为2的等边三角形,则该四棱锥的四条侧棱长之和等于4$\sqrt{5}$.