题目内容
6.已知复数z1=a+bi,z2=-1+ai(a,b∈R),若|z1|<|z2|,则( )| A. | b<-1或b>1 | B. | -1<b<1 | C. | b>1 | D. | b>0 |
分析 由题意可得a2+b2<1+a2,化简可得 b2<1,求解不等式得答案.
解答 解:∵z1=a+bi,z2=-1+ai(a,b∈R),且|z1|<|z2|,
∴a2+b2<1+a2,化简可得 b2<1,解得-1<b<1.
∴b的取值范围是(-1,1).
故选:B.
点评 本题考查复数模的求法,考查了不等式的解法,是基础题.

练习册系列答案
相关题目
16.函数y=$\sqrt{{x^2}-8x+20}$+$\sqrt{{x^2}+1}$的最小值为( )
| A. | 12 | B. | 25 | C. | 8 | D. | 5 |
1.数列{an}满足an+1+(-1)nan=2n-1,则{an}的前80项和为( )
| A. | 3690 | B. | 3660 | C. | 3240 | D. | 1830 |
16.在正三角形ABC中,D是BC上的点,且AB=4,BD=1,则$\overrightarrow{AB}$•$\overrightarrow{AD}$=( )
| A. | 4 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 14 |
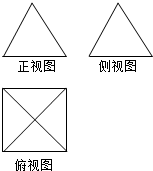 若一个四梭锥的三视图如图所示,其中正视图与侧视图都是边长为2的等边三角形,则该四棱锥的四条侧棱长之和等于4$\sqrt{5}$.
若一个四梭锥的三视图如图所示,其中正视图与侧视图都是边长为2的等边三角形,则该四棱锥的四条侧棱长之和等于4$\sqrt{5}$.