题目内容
14.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4,x≤0}\\{x+\frac{1}{x},x>0}\end{array}\right.$,若关于x的方程f(2x+$\frac{1}{2}$)=m有3个不同的解,则m的取值范围是(2,4].分析 令t=2x+$\frac{1}{2}$,则f(t)=m,作出函数f(x)的图象,结合一次方程的根的个数,即可得到m的范围.
解答 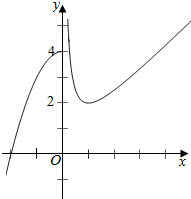 解:令t=2x+$\frac{1}{2}$,
解:令t=2x+$\frac{1}{2}$,
则f(t)=m,
当t≤0时,f(t)≤4;当t>0时,f(t)≥2;
由图象可得,当m<2时,t有一解;
当m=2时,t有两解;
当2<m≤4时,t有三解;
当m>4时,t有两解.
当m<2时,t=2x+$\frac{1}{2}$一个根;
当m=2时,t=2x+$\frac{1}{2}$,方程有两个实根;
当2<m≤4时,t=2x+$\frac{1}{2}$有三个根;
当m>4时,t=2x+$\frac{1}{2}$有两个不同的实根.
综上可得m的范围是(2,4].
故答案为:(2,4].
点评 本题考查函数的性质和运用,主要考查函数的零点的判断,注意运用数形结合的思想方法,属于中档题.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
4.F1,F2分别为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的左右焦点,P为椭圆上一动点,F2关于直线PF1的对称点为M,F1关于直线PF2的对称点为N,则当|MN|最大时,S${\;}_{△P{F}_{1}{F}_{2}}$为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
5.函数f(x)=lgx-$\frac{9}{x}$的零点所在的区间是( )
| A. | (10,100) | B. | ($\sqrt{10}$,10) | C. | (1,$\sqrt{10}$) | D. | (0,1) |
2.已知直线l与直线2x-3y+4=0关于直线x=1对称,则直线l的方程为( )
| A. | 2x+3y-8=0 | B. | 3x-2y+1=0 | C. | x+2y-5=0 | D. | 3x+2y-7=0 |
4.设等比数列{an}的前n项和为Sn,若8a2+a5=0,则下列式子中数值不能确定的是( )
| A. | $\frac{{a}_{5}}{{a}_{2}}$ | B. | $\frac{{S}_{5}}{{S}_{3}}$ | C. | $\frac{{a}_{n+1}}{{a}_{n}}$ | D. | $\frac{{S}_{n+1}}{{S}_{n}}$ |
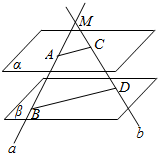 如图所示,α∥β,M在α与β同侧,过M作直线a与b,a分别与α、β相交于A、B,b分别与α、β相交于C、D.
如图所示,α∥β,M在α与β同侧,过M作直线a与b,a分别与α、β相交于A、B,b分别与α、β相交于C、D.