题目内容

在Rt△ABC中，CA=CB=3，M，N是斜边AB上的两个动点，且MN=
2
，则
CM
•
CN
的取值范围为（　　）
A、[2，
5
2
]
B、[2，4]
C、[3，6]
D、[4，6]
考点：平面向量数量积的运算
专题：平面向量及应用
分析：通过建立直角坐标系求出AB所在直线的方程，设出M，N的坐标，将
CM
•
CN
=2（b-1）2，0≤b≤1，求出范围．
解答： 解：以C为坐标原点，CA为x轴建立平面坐标系，

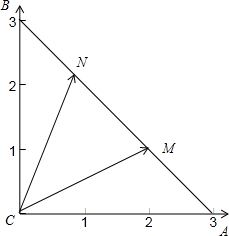
则A（30），B（0，3，
∴AB所在直线的方程为：y=3-x，
设M（a，3-a），N（b，3-b），且0≤a≤3，0≤b≤3不妨设a＞b，
∵MN=
2
，
∴（a-b）2+（b-a）2=2，
∴a-b=1，
∴a=b+1，
∴0≤b≤2，
∴
CM
•
CN
=（a，3-a）•（b，3-b）
=2ab-3（a+b）+9
=2（b2-2b+3），0≤b≤2，
∴b=1时有最小值4；
当b=0，或b=2时有最大值6，
∴
CM
•
CN
的取值范围为[4，6]
故选：D
点评：熟练掌握通过建立直角坐标系、数量积得坐标运算是解题的关键．
练习册系列答案
相关题目
f（x）在R上满足f（x）=-f（x+
3
2
），f（1）=0，则f（10）=
 
．
设函数f（x）=|x-4|+|x-a|，x∈R．
（1）证明：当a=1时，不等式lnf（x）＞1成立；
（2）关于x的不等式f（x）≥a在R上恒成立，求实数a的最大值．
设函数f（x）=n-1，x∈[n，n+1），n∈N，函数g（x）=log2x，则方程f（x）=g（x）实数根的个数是（　　）
A、1个B、2个C、3个D、4个
设f（x）是定义在D上的函数，若对任何实数α∈（0，1）以及D中的任意两数x1、x2，恒有f（αx1+（1-α）x2）≤αf（x1）+（1-α）f（x2），则称f（x）为定义在D上的C函数．
（1）证明函数f1(x)=x2是定义域上的C函数；
（2）判断函数f2(x)=
1
x
(x＜0)是否为定义域上的C函数，请说明理由；
（3）若f（x）是定义域为R的函数，且最小正周期为T，试证明f（x）不是R上的C函数．
为了加强环保建设，提高社会效益和经济效益，某市计划用若干年时间更换一万辆燃油型公交车．每更换一辆新车，则淘汰一辆旧车，更换的新车为电力型车和混合动力型车．今年初投入了电力型公交车128辆，混合动力型公交车400辆，计划以后电力型车每年的投入量比上一年增加50%，混合动力型车每年比上一年多投入a辆．设an、bn分别为第n年投入的电力型公交车、混合动力型公交车的数量，设Sn、Tn分别为n年里投入的电力型公交车、混合动力型公交车的总数量．
（1）求Sn、Tn，并求n年里投入的所有新公交车的总数Fn；
（2）该市计划用7年的时间完成全部更换，求a的最小值．
O是平面上一点，A、B、C是平面上不共线三点，动点P满足：
OP
=
OA
+λ（
AB
+
AC
），λ∈[-1，2]，已知λ=1时，|
AP
|=2，则
PA
•
PB
+
PA
•
PC
的最大值为（　　）
A、-2B、24C、48D、96
若函数f（x）=sinωx+
3
cosωx，x∈R，又f（a）=2，f（β）=0，|α-β|的最小值等于
5π
4
，则正数ω的值为（　　）
A、
8
5
B、
4π
5
C、
2
5
D、
2π
5
已知an=
1
2n
cos
nπ
2
，则无穷数列{an}前n项和的极限为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网