题目内容
若△ABC的定点B,C的坐标分别为(-4,0),(4,0),AC、AB边上的中线长之和为15,则△ABC的重心G的轨迹方程为 .
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据三角形重心的性质可得G到B、C两点的距离之和等于10,因此G的轨迹为以B、C为焦点的椭圆.利用题中数据加以计算可得相应的椭圆方程,注意到点G不能落在x轴上得到答案.
解答:
解: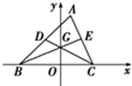 设AC、AB边上的中线分别为CD、BE
设AC、AB边上的中线分别为CD、BE
∵BG=
BE,CG=
CD
∴BG+CG=
(BE+CD)=10(定值)>8
因此,G的轨迹为以B、C为焦点的椭圆,2a=10,c=4
∴a=5,b=3,可得椭圆的方程为
+
=1
∵当G点在x轴上时,A、B、C三点共线,不能构成△ABC
∴G的纵坐标不能是0,可得△ABC的重心G的轨迹方程为
+
=1(y≠0)
故答案为:
+
=1(y≠0).
 设AC、AB边上的中线分别为CD、BE
设AC、AB边上的中线分别为CD、BE∵BG=
| 2 |
| 3 |
| 2 |
| 3 |
∴BG+CG=
| 2 |
| 3 |
因此,G的轨迹为以B、C为焦点的椭圆,2a=10,c=4
∴a=5,b=3,可得椭圆的方程为
| x2 |
| 25 |
| y2 |
| 9 |
∵当G点在x轴上时,A、B、C三点共线,不能构成△ABC
∴G的纵坐标不能是0,可得△ABC的重心G的轨迹方程为
| x2 |
| 25 |
| y2 |
| 9 |
故答案为:
| x2 |
| 25 |
| y2 |
| 9 |
点评:本题给出三角形两条中线长度之和等于定值,求重心G的轨迹方程.着重考查了三角形重心的性质、椭圆的定义与标准方程和轨迹方程的求法等知识,属于中档题.

练习册系列答案
相关题目
已知f(x)是偶函数,对任意的a,b∈[0,+∞)都有
<0,若f(lgx)>f(1),则x的取值范围是( )
| f(a)-f(b) |
| a-b |
A、、(
| ||
B、(0,
| ||
C、(
| ||
| D、(0,1)∪(10,+∞x1x2=1 ) |
在复平面内,复数z=
+i2013表示的点所在的象限是( )
| i |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |