题目内容
20.对于函数f(x),若存在x0∈R,使f(x0)=x0,则称x0是f(x)的一个不动点,已知函数f(x)=ax2+(b+1)x+(b-1)(a≠0),(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
分析 (1)将a、b代入函数,根据条件“若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点”建立方程解之即可;
(2)对任意实数b,f(x)恒有两个相异不动点转化成对任意实数b,ax2+(b+1)x+b-1=x恒有两个不等实根,再利用判别式建立a、b的不等关系,最后将b看成变量,转化成关于b的恒成立问题求解即可.
解答 解:(1)当a=1,b=-2时,
f(x)=x2-x-3=x?x2-2x-3=0
?(x-3)(x+1)=0?x=3或x=-1,
∴f(x)的不动点为x=3或x=-1.
(2)对任意实数b,f(x)恒有两个相异不动点
?对任意实数b,ax2+(b+1)x+b-1=x,
即ax2+bx+b-1=0恒有两个不等实根,
?对任意实数b,△=b2-4a(b-1)>0恒成立,
?对任意实数b,b2-4ab+4a>0恒成立,
?△′=(4a)2-4×4a<0
?a2-a<0
?0<a<1.
即a的取值范围是0<a<1.
点评 本题主要考查了函数与方程的综合运用,以及恒成立问题的处理,属于中档题.

练习册系列答案
相关题目
11.若椭圆的焦距与短轴长相等,则此椭圆的离心率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
8.如图所示y=sin(ωx+φ)的图象可以由y=sinωx的图象沿x轴经怎样的平移得到的( )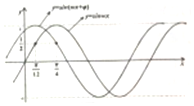

| A. | 沿x轴向左平移$\frac{π}{6}$个单位 | B. | 沿x轴向左平移$\frac{π}{3}$个单位 | ||
| C. | 沿x轴向右平移$\frac{π}{6}$个单位 | D. | 沿x轴向右平移$\frac{π}{6}$个单位 |
15.某箱子的容积V(x)与底面边长x的关系为$V(x)={x^2}•(\frac{60-x}{2})$,则当箱子的容积最大时,箱子底面边长为( )
| A. | 30 | B. | 40 | C. | 50 | D. | 以上都不正确 |