题目内容
20．已知幂函数y=xn的图象经过点（2，8），则此幂函数的解析式是（ ）| A． | y=2x | B． | y=3x | C． | y=x3 | D． | y=x-1 |
分析 设出幂函数的解析式，带入点的坐标，求出函数的解析式即可．
解答 解：设幂函数为f（x）=xα，
因为图象经过点（2，8），
∴f（2）=8=23，从而α=-3函数的解析式f（x）=x3，
故选：C．
点评 本题考查了求幂函数的解析式问题，待定系数法是常用方法之一，本题是一道基础题．
练习册系列答案
相关题目
11．与α=$\frac{π}{12}$+2kπ（k∈Z）终边相同的角是（ ）
| A． | 345° | B． | 375° | C． | -$\frac{11}{12}$π | D． | $\frac{23}{12}$π |
8．设全集U={1，2，3，4，5，6}，A={1，2}，B={2，3，4}，则A∩（∁UB）=（ ）
| A． | {1，2，5，6} | B． | {1，2，3，4} | C． | {2} | D． | {1} |
15．已知三棱柱ABC-A1B1C1的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为$\sqrt{3}$，BC=$\sqrt{3}$，AC=1，∠ACB=90°，则此球的体积等于（ ）
| A． | $\frac{40\sqrt{10}}{3}$π | B． | $\frac{64\sqrt{2}}{3}$π | C． | $\frac{8\sqrt{2}}{3}$π | D． | 8π |
5．函数f（x）=x-log${\;}_{\frac{1}{2}}$x的零点个数为（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 无数多个 |
12．函数f（x）=$\frac{1}{\sqrt{1-{2}^{x}}}$的定义域是（ ）
| A． | （-∞，$\frac{1}{2}$） | B． | （-∞，0] | C． | （0，+∞） | D． | （-∞，0） |
9．已知集合A={1，4}，B={y|y=log2x，x∈A}，则A∪B=（ ）
| A． | {1，4} | B． | {0，1，4} | C． | {0，2} | D． | {0，1，2，4} |
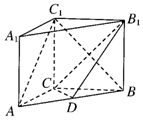如图所示，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D是AB的中点．