题目内容
已知奇函数f(x)在其定义域(-2,2)上单调递减,则不等式f(x-1)+f(3-2x)≤0的解集是 .
考点:奇偶性与单调性的综合
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:根据函数是奇函数,把不等式f(x-1)+f(3-2x)≤0变形,再利用函数的单调性,化抽象不等式为具体不等式,解之即可.
解答:
解:∵奇函数f(x),不等式f(x-1)+f(3-2x)≤0,
∴f(x-1)≤-f(3-2x)=f(2x-3),
∵f(x)在(-2,2)上单调递减,
∴
,即有
,
解得:
<x≤2,
则原不等式的解集为:(
,2].
故答案为:(
,2].
∴f(x-1)≤-f(3-2x)=f(2x-3),
∵f(x)在(-2,2)上单调递减,
∴
|
|
解得:
| 1 |
| 2 |
则原不等式的解集为:(
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:本题考查函数单调性与奇偶性的结合,考查抽象不等式的解法,解题的关键是正确运用函数的单调性.属于中档题和易错题.

练习册系列答案
相关题目
在空间中,下列命题正确的是( )
| A、三条直线两两相交,则这三条直线确定一个平面 |
| B、若平面α⊥β,且α∩β=l,则过α内一点P与l垂直的直线垂直于平面β |
| C、若直线m与平面α内的一条直线平行,则m∥α |
| D、若直线a与直线b平行,且直线l⊥a,则l∥b |
若实数a,b,c,d满足(b+a2•3lna)2+(c•d+2)2=0,且a∈(0,1),则(a•c)2+(b•d)2的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设F1,F2是椭圆
+
=1的两焦点,M为椭圆上的点,若MF1⊥MF2,则△MF1F2的面积为( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、4 | ||
| B、8 | ||
C、4
| ||
D、8
|
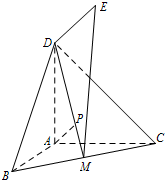 如图,DA⊥平面ABC,ED⊥平面BCD,DE=DA=AB=AC,∠BAC=120°,M为BC中点.
如图,DA⊥平面ABC,ED⊥平面BCD,DE=DA=AB=AC,∠BAC=120°,M为BC中点.