题目内容
11.如图表示某正弦曲线的一段图象,求函数的解析式.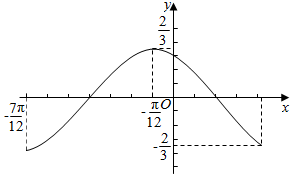
分析 利用函数的图象经过的最大值求出A,周期求出ω,利用函数的图象结果的特殊点求出φ,即可求出函数的解析式.
解答 解:由图象可知:A=$\frac{2}{3}$,$\frac{1}{2}$T=-$\frac{π}{12}$-($-\frac{7π}{12}$),
∴T=π
∴ω=$\frac{2π}{T}$=2,
函数的图象经过(-$\frac{π}{12}$,$\frac{2}{3}$),
∴$\frac{2}{3}$sin(2×(-$\frac{π}{12}$)+φ)=$\frac{2}{3}$,
∴-$\frac{π}{6}$+φ=$\frac{π}{2}$,
∴φ=$\frac{2π}{3}$,
∴f(x)=$\frac{2}{3}$sin(2x+$\frac{2π}{3}$).
点评 本题考查函数的解析式的求法,三角函数的图象的应用,考查学生的识图用图能力.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 已知函数f(x)=-mcos(ωx+φ)(m>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,点A,B,C为f(x)的图象与坐标轴的交点,且A(1,0),D($\frac{5}{3}$,-$\frac{10}{3}$),$\overrightarrow{CD}$=$\frac{1}{2}$$\overrightarrow{DB}$,则m=5$\sqrt{2}$.
已知函数f(x)=-mcos(ωx+φ)(m>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,点A,B,C为f(x)的图象与坐标轴的交点,且A(1,0),D($\frac{5}{3}$,-$\frac{10}{3}$),$\overrightarrow{CD}$=$\frac{1}{2}$$\overrightarrow{DB}$,则m=5$\sqrt{2}$.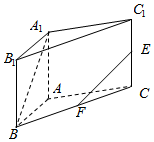 直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=2$\sqrt{2}$,E,F分别是CC1,BC的中点,求:
直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=2$\sqrt{2}$,E,F分别是CC1,BC的中点,求: