题目内容
2.已知函数f(x)=(-x2+ax)e-x,若a=2时,求以点P(0,0)为切点的切线方程.分析 求出函数f(x)的导数,求得切线的斜率,再由斜截式方程,即可得到所求切线方程.
解答 解:a=2时,f(x)=(-x2+2x)e-x,
f′(x)=(-2x+2)•e-x-(-x2+2x)•e-x
=(x2-4x+2)•e-x,
以点P(0,0)为切点的切线的斜率为k=2,
则以点P(0,0)为切点的切线方程为y=2x.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,正确求导和运用直线方程是解题的关键.

练习册系列答案
相关题目
12.已知a=cos3,b=2${\;}^{\frac{1}{3}}$,c=($\frac{1}{3}$)2,那么( )
| A. | a<b<c | B. | c<b<a | C. | a<c<b | D. | c<a<b |
19.一个几何体的三视图如图所示,则该几何体的表面积为( )
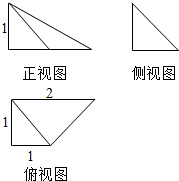

| A. | $\frac{3}{2}$ | B. | $\frac{{6+\sqrt{2}+\sqrt{6}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{3+\sqrt{2}+\sqrt{6}}}{2}$ |
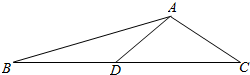 在△ABC中,∠BAD=30°,AB=4,AC=2,点D在BC上,且BC=2BD
在△ABC中,∠BAD=30°,AB=4,AC=2,点D在BC上,且BC=2BD