题目内容
12.已知a=cos3,b=2${\;}^{\frac{1}{3}}$,c=($\frac{1}{3}$)2,那么( )| A. | a<b<c | B. | c<b<a | C. | a<c<b | D. | c<a<b |
分析 别判断a,b,c的取值范围,然后确定a,b,c的大小关系.
解答 解:∵a=cos3<0,
b=2${\;}^{\frac{1}{3}}$>1,
0<c=($\frac{1}{3}$)2<1,
∴a<c<b,
故选:C.
点评 本题主要考查函数值的大小比较,利用指数函数,三角函数的性质确定取值范围是解决本题的关键,比较基础.

练习册系列答案
相关题目
3.已知数列{an}{n=1,2,3…,2015},圆C1:x2+y2-4x-4y=0,圆C2:x2+y2-2anx-2a2006-ny=0,若圆C2平分圆C1的周长,则{an}的所有项的和为( )
| A. | 2014 | B. | 2015 | C. | 4028 | D. | 4030 |
1.若${∫}_{0}^{1}$(x2+mx)dx=$\frac{4}{3}$,则在(x2-3x+m)5的展开式中,含x项的系数为( )
| A. | -240 | B. | -120 | C. | 0 | D. | 120 |
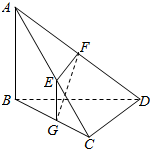 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证:
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,E,F,G分别是AC,AD,BC的中点.求证: