题目内容
不等式3≤|5-2x|＜9的解集为（ ）
| A、（-2，1] |
| B、[-1，1] |
| C、[4，7） |
| D、（-2，1]∪[4，7） |
考点：其他不等式的解法
专题：不等式的解法及应用
分析：由不等式可得3≤2x-5＜9 或-9＜2x-5≤-3，由此求得不等式的解集．
解答：
解：由不等式3≤|5-2x|＜9 可得3≤2x-5＜9 或-9＜2x-5≤-3，
解得 4≤x＜7，或-2＜x≤1，
故选：D．
解得 4≤x＜7，或-2＜x≤1，
故选：D．
点评：本题主要考查绝对值不等式的解法，体现了等价转化的数学思想，属于中档题．
练习册系列答案
相关题目
直线y=kx+b与圆（x-1）2+（y-2）2=5有公共点的一个充分不必要条件为（ ）
| A、b≤4 | B、b≥0 |
| C、-4≤b≤4 | D、0≤b≤4 |
将函数y=sin(2x+
)的图象向左平移
个单位，再向上平移2个单位，则所得函数的表达式是（ ）
| π |
| 4 |
| π |
| 4 |
A、y=sin(2x-
| ||
B、y=cos(2x+
| ||
C、y=sin(2x+
| ||
D、y=cos(2x-
|
若b为a，c的等比中项，则函数y=ax2+bx+c的零点个数是（ ）
| A、0 | B、1 |
| C、2 | D、A、B、C都有可能 |
已知tanα=-
，则sin2α-2cos2α-1=（ ）
| 1 |
| 2 |
A、-
| ||
B、-
| ||
C、-
| ||
| D、-2 |
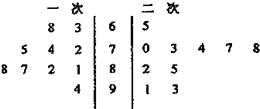如图是某同学一学期两次考试成绩的茎叶图，现从该同学两次考试成绩中各取一科成绩，则这两科成绩都在80分以上的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|