题目内容
4.已知各项均为正数的数列{an}的前n项和为Sn,满足a${\;}_{n+1}^{2}$=2Sn+n+4,且a2-1,a3,a7恰为等比数列{bn}的前3项.(1)求数列{an},{bn}的通项公式;
(2)令cn=$\frac{n}{{b}_{n}}$-$\frac{1}{{a}_{n}{a}_{n+1}}$,求数列{cn}的前n项和Tn.
分析 (1)将n换为n-1,两式相减,可得an+1-an=1,即公差d=1,再由等比数列的性质和等差数列的通项公式,解方程可得a2=3,再由等差数列的通项公式可得通项;再由等比数列的定义和通项公式可得所求;
(2)求得cn=$\frac{n}{{b}_{n}}$-$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{n}{{2}^{n}}$-$\frac{1}{(n+1)(n+2)}$=$\frac{n}{{2}^{n}}$-($\frac{1}{n+1}$-$\frac{1}{n+2}$),分别运用数列的求和方法:错位相减法和裂项相消求和,计算即可得到所求和.
解答 解:(1)当n=1时,a22=2S1+1+4=2a1+5,
当n>1时,an+12=2Sn+n+4,①
可得an2=2Sn-1+n-1+4,②
①-②可得,an+12-an2=2an+1,
即有an+12=(an+1)2,
数列{an}的各项均为正数,
可得an+1-an=1,即公差d=1,
由a2-1,a3,a7恰为等比数列{bn}的前3项,
可得a32=(a2-1)a7,
即为(a2+1)2=(a2-1)(a2+5),解得a2=3,
则an=a2+n-2=n+1;b1=a2-1=2,公比q=$\frac{{a}_{7}}{{a}_{3}}$=$\frac{8}{4}$=2,
则bn=b1qn-1=2n;
(2)cn=$\frac{n}{{b}_{n}}$-$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{n}{{2}^{n}}$-$\frac{1}{(n+1)(n+2)}$=$\frac{n}{{2}^{n}}$-($\frac{1}{n+1}$-$\frac{1}{n+2}$),
前n项和Tn=(1•$\frac{1}{2}$+2•$\frac{1}{4}$+…+n•($\frac{1}{2}$)n)-($\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n+1}$-$\frac{1}{n+2}$),
由Fn=1•$\frac{1}{2}$+2•$\frac{1}{4}$+…+n•($\frac{1}{2}$)n,
$\frac{1}{2}$Fn=1•$\frac{1}{4}$+2•$\frac{1}{8}$+…+n•($\frac{1}{2}$)n+1,
两式相减可得,$\frac{1}{2}$Fn=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+($\frac{1}{2}$)n-n•($\frac{1}{2}$)n+1
=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$--n•($\frac{1}{2}$)n+1
化简可得,Fn=2-$\frac{n+2}{{2}^{n}}$,
则Tn=2-$\frac{n+2}{{2}^{n}}$-($\frac{1}{2}$-$\frac{1}{n+2}$)=$\frac{3}{2}$-$\frac{n+2}{{2}^{n}}$+$\frac{1}{n+2}$.
点评 本题考查等差数列和等比数列的通项和求和公式的运用,考查数列的求和方法:错位相减法和裂项相消求和,考查运算能力,属于中档题.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
以上推理的错误是( )
| A. | 大前提错误导致结论错误 | B. | 小前提错误导致结论错误 | ||
| C. | 推理形式错误导致结论错误 | D. | 大前提和小前提错误导致结论错误 |
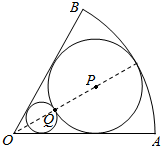 如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.
如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.