题目内容
已知实数x、y满足
,则目标函数z=
的最大值与最小值的和是 .
|
| x+4y+5 |
| x+1 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用目标函数的几何意义即可得到结论.
解答:
解:z=
=
=1+4×
,
设k=
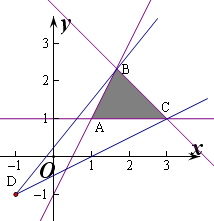
,则k的几何意义是区域内的点到定点D(-1,-1)的斜率,
则z=1+4k,
作出不等式组对应的平面区域如图:
则DB的斜率最大,DC的斜率最小,
由
,解得
,即C(3,1),此时k=
=
,
由
,解得
,即B(
,
),此时k=
=
,
即
≤k≤
,
则2≤4k≤5,3≤1+4k≤6,
故3≤z≤6,
则z的最大值与最小值的和为3+6=9,
故答案为:9
| x+4y+5 |
| x+1 |
| x+1+4(y+1) |
| x+1 |
| y+1 |
| x+1 |

设k=
| y+1 |
| x+1 |
则z=1+4k,
作出不等式组对应的平面区域如图:
则DB的斜率最大,DC的斜率最小,
由
|
|
| 1+1 |
| 3+1 |
| 1 |
| 2 |
由
|
|
| 5 |
| 3 |
| 7 |
| 3 |
| ||
|
| 5 |
| 4 |
即
| 1 |
| 2 |
| 5 |
| 4 |
则2≤4k≤5,3≤1+4k≤6,
故3≤z≤6,
则z的最大值与最小值的和为3+6=9,
故答案为:9
点评:本题主要考查了用平面区域二元一次不等式组,以及直线斜率的计算,利用数形结合是解决本题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
某单位共有老、中、青职工860人,其中青年职工320人,中年职工人数是老年职工人数的2倍.为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工64人,则该样本中的老年职工人数为 .
已知M(x0,y0)是圆x2+y2=a2外任意一点,则直线x0x+y0y=a2与该圆的位置关系是( )
| A、相切 |
| B、相交 |
| C、相离 |
| D、由点(x0、y0)的位置决定 |
 如图,有一块扇形草地OMN,已知半径为R,
如图,有一块扇形草地OMN,已知半径为R,