题目内容
已知集合M={（x，y）|0≤y≤| 4-x2 |
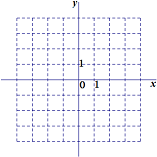
（1）在坐标平面内作出集合M所表示的平面区域；
（2）若点P（x，y）∈M，求（x+3）2+（y-3）2的取值范围．
考点：集合的表示法
专题：集合
分析：（1）根据题意画出图形即可；
（2）结合（1）找出（x+3）2+（y-3）2表示的意义求解即可．
（2）结合（1）找出（x+3）2+（y-3）2表示的意义求解即可．
解答：
解：（ I） 如图
区域内部即为所求；
（ II）由题意可得：
区域内的点到（-3，3）的距离的平方，
所以（x+3）2+（y-3）2∈[22-12
，34]．
区域内部即为所求；（ II）由题意可得：
区域内的点到（-3，3）的距离的平方，
所以（x+3）2+（y-3）2∈[22-12
| 2 |
点评：本题主要考查集合的含义以及两点间的距离公式的应用，属于基础题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
设等差数列{an}的前n项为Sn，已知a1=-11，a3+a7=-6，当Sn取最小值时，n=（ ）
| A、5 | B、6 | C、7 | D、8 |
设a=70.3，b=0.37，c=log70.3，则a，b，c的大小关系是（ ）
| A、b＜c＜a |
| B、c＜b＜a |
| C、c＜a＜b |
| D、a＜b＜c |
下列有关命题的说法正确的是（ ）
| A、命题“?x∈R，均有x2-x+1＞0”的否定是：“?x∈R，使得x2-x+1＜0” | ||||||
| B、“x=3”是“2x2-7x+3=0”成立的充分不必要条件 | ||||||
C、线性回归方程
| ||||||
| D、若“p∨（?q）”为真命题，则“p∧q”也为真命题 |
