题目内容
函数y=x+
(x>2)的最小值是 .
| 3 |
| x-2 |
考点:基本不等式
专题:不等式的解法及应用
分析:变形利用基本不等式的性质即可得出.
解答:
解:∵x>2,∴x-2>0.
∴函数y=x+
=(x-2)+
+2≥2
+2=2
+2,当且仅当x=
+2时取等号.
∴函数y=x+
(x>2)的最小值是2+2
.
故答案为:2+2
.
∴函数y=x+
| 3 |
| x-2 |
| 3 |
| x-2 |
(x-2)•
|
| 3 |
| 3 |
∴函数y=x+
| 3 |
| x-2 |
| 3 |
故答案为:2+2
| 3 |
点评:本题考查了基本不等式的性质,属于基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
当生物死亡时,他机体内原有的碳14含量按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”,据此规律,生物体内碳14的含量P与死亡年数t间的函数关系式为( )
A、P=(
| ||||
B、P=(
| ||||
C、P=(
| ||||
D、P=(
|
已知函数f(x)=(a2-a-1)x
为幂函数,则a=( )
| 1 |
| a-2 |
| A、-1 或 2 |
| B、-2 或 1 |
| C、-1 |
| D、1 |
已知Sn是等差数列{an}的前n项和,若a1=-2014,
-
=6,则S2013等于( )
| S2014 |
| 2014 |
| S2008 |
| 2008 |
| A、2013 | B、-2013 |
| C、-4026 | D、4026 |
已知点A(1,
),B(-1,3
),则直线AB的倾斜角是( )
| 3 |
| 3 |
| A、60° | B、30° |
| C、120° | D、150° |
已知全集U={1,2,3,4,5},集合A={1,2,3},则∁UA=( )
| A、{4,5} |
| B、{1,2,3} |
| C、{5} |
| D、{2,4} |
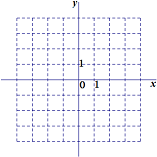 已知集合M={(x,y)|0≤y≤
已知集合M={(x,y)|0≤y≤