题目内容
11.在△ABC中,a,b,c分别是角A,B,C的对边,已知a2+c2=ac+b2,b=$\sqrt{3}$,且a≥c,则2a-c的最小值是$\sqrt{3}$.分析 使用余弦定理求出B,由正弦定理用A,C表示出a,c根据A的范围和正弦函数的性质得出2a-c的范围.
解答 解:在△ABC中,∵a2+c2=ac+b2,∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{2}$,
∴B=$\frac{π}{3}$.∴A+C=$\frac{2π}{3}$,
由正弦定理得:$\frac{a}{sinA}=\frac{c}{sinC}=\frac{b}{sinB}$=2.
∴a=2sinA,c=2sinC=2sin($\frac{2π}{3}-A$)=$\sqrt{3}$cosA+sinA,
∴2a-c=3sinA-$\sqrt{3}$cosA=2$\sqrt{3}$sin(A-$\frac{π}{6}$).
∵a≥c,∴$\frac{π}{3}$≤A<$\frac{2π}{3}$.
∴当A=$\frac{π}{3}$时,2a-c取得最小值2$\sqrt{3}$sin$\frac{π}{6}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了正余弦定理在解三角形中的应用,属于中档题.

练习册系列答案
相关题目
19.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的最小值为-2,且对于任意x∈R,恒有f(x+$\frac{π}{2}$)+f(x)=0,又f(0)=1,则函数f(x)在区间[0,π]上的增区间为( )
| A. | [0,$\frac{π}{6}$] | B. | [$\frac{π}{6}$,$\frac{2π}{3}$] | C. | [0,$\frac{π}{6}$]∪[$\frac{2π}{3}$,π] | D. | [0,$\frac{π}{6}$]和[$\frac{2π}{3}$,π] |
3.已知F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,且双曲线C的焦距为2c,定点G(0,c),若双曲线C上存在点P满足|PF|=|PG|,则双曲线的离心率的取值范围是( )
| A. | ($\sqrt{2}$,+∞) | B. | (1,$\sqrt{2}$) | C. | [$\sqrt{3}$,+∞) | D. | (1,$\sqrt{3}$) |
20.已知f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,则满足f(a)-f(-a)<1的a的取值范围是( )
| A. | (-∞,3) | B. | (-∞,log23) | C. | (3,+∞) | D. | (log23,+∞) |
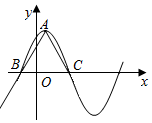 函数f(x)=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.