题目内容
已知函数f(x)=(x2-2x)•lnx+ax2+2
(1)当a=-1时,求f(x)在(1,f(1))处的切线方程;
(2)设函数g(x)=f(x)-x-2,若函数g(x)有且仅有一个零点时,求a的值.
(1)当a=-1时,求f(x)在(1,f(1))处的切线方程;
(2)设函数g(x)=f(x)-x-2,若函数g(x)有且仅有一个零点时,求a的值.
考点:利用导数研究曲线上某点切线方程,函数的零点
专题:导数的综合应用
分析:(1)当a=-1时,求函数的导数,根据导数的几何意义即可求f(x)在(1,f(1))处的切线方程;
(2)构造函数,求函数的导数,判断函数的极值即可得到结论.
(2)构造函数,求函数的导数,判断函数的极值即可得到结论.
解答:
解:(1)当a=-1时,f(x)=(x2-2x)•lnx-x2+2,
则f′(x)=(2x-2)lnx+(x-2)-2x,
∴f′(1)=-3,f(1)=1,
则f(x)在(1,f(1))处的切线方程为3x+y-4=0;
(2)由g(x)=f(x)-x-2=0,得(x2-2x)•lnx+ax2+2=x+2,
即a=
,
设h(x)=
,
则h′(x)=-
-
+
=
,
令t(x)=1-x-2lnx,
则t′(x)=-1-
=
,
∵t′(x)<0,t(x)在(0,+∞)上是减函数,t(1)=h'(1)=0,
∴当0<x<1时,h′(x)>0,
当x>1时,h′(x)<0,
即h(x)的最大值为h(1)=1,
∴若函数g(x)有且仅有一个零点时,则a=1.
则f′(x)=(2x-2)lnx+(x-2)-2x,
∴f′(1)=-3,f(1)=1,
则f(x)在(1,f(1))处的切线方程为3x+y-4=0;
(2)由g(x)=f(x)-x-2=0,得(x2-2x)•lnx+ax2+2=x+2,
即a=
| 1-(x-2)lnx |
| x |
设h(x)=
| 1-(x-2)lnx |
| x |
则h′(x)=-
| 1 |
| x2 |
| 1 |
| x |
| 2-2lnx |
| x2 |
| 1-x-2lnx |
| x2 |
令t(x)=1-x-2lnx,
则t′(x)=-1-
| 2 |
| x |
| -x-2 |
| x |
∵t′(x)<0,t(x)在(0,+∞)上是减函数,t(1)=h'(1)=0,
∴当0<x<1时,h′(x)>0,
当x>1时,h′(x)<0,
即h(x)的最大值为h(1)=1,
∴若函数g(x)有且仅有一个零点时,则a=1.
点评:本题主要考查导数的综合应用,考查导数的几何意义以及函数单调性与导数之间的关系,考查学生的运算能力.

练习册系列答案
相关题目
如图,在圆C:x2+y2=10内随机撒一粒豆子,则豆子落在阴影部分的概率是( )


A、1-
| ||
B、
| ||
C、
| ||
D、
|
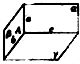
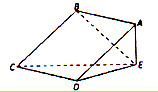 如图所示四棱锥E-ABCD中,四边形ABCD为正方形,AE⊥平面CDB,且AR=3,
如图所示四棱锥E-ABCD中,四边形ABCD为正方形,AE⊥平面CDB,且AR=3,