题目内容
等差数列{an}中,2a1+3a2=11,2a3=a2+a6-4,其前n项和为Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足bn=an•2n-1,求{bn}的前n项和Tn.
(理)(Ⅲ)若数列{cn}满足cn=
,且{cn}前n项和为Ln,求证:Ln<
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足bn=an•2n-1,求{bn}的前n项和Tn.
(理)(Ⅲ)若数列{cn}满足cn=
| 1 |
| Sn+1-1 |
| 3 |
| 4 |
考点:数列的求和
专题:等差数列与等比数列
分析:(I)利用等差数列的通项公式即可得出;
(II)利用“错位相减法”即可得出;
(III)利用“裂项求和”即可得出.
(II)利用“错位相减法”即可得出;
(III)利用“裂项求和”即可得出.
解答:
解:(I)设等差数列{an}的公差为d,
∵2a1+3a2=11,2a3=a2+a6-4,∴
,解得a1=1,d=2.
∴an=1+2(n-1)=2n-1.
(II)bn=an•2n-1=(2n-1)•2n-1.
∴{bn}的前n项和Tn=1+3×2+5×22-…+(2n-1)•2n-1.
2Tn=2+3×22+…+(2n-3)•2n-1+(2n-1)•2n
∴-Tn=1+2×2+2×22+…+2×2n-1-(2n-1)•2n=
-1-(2n-1)•2n=(3-2n)•2n-3.
∴Tn=(2n-3)•2n+3.
(III)Sn=
=n2,
∴cn=
=
=
=
(
-
).
∴Ln=
[(1-
)+(
-
)+(
-
)+…+(
-
)+(
-
)]
=
(1+
-
-
)<
.
∵2a1+3a2=11,2a3=a2+a6-4,∴
|
∴an=1+2(n-1)=2n-1.
(II)bn=an•2n-1=(2n-1)•2n-1.
∴{bn}的前n项和Tn=1+3×2+5×22-…+(2n-1)•2n-1.
2Tn=2+3×22+…+(2n-3)•2n-1+(2n-1)•2n
∴-Tn=1+2×2+2×22+…+2×2n-1-(2n-1)•2n=
| 2(2n-1) |
| 2-1 |
∴Tn=(2n-3)•2n+3.
(III)Sn=
| n(1+2n-1) |
| 2 |
∴cn=
| 1 |
| Sn+1-1 |
| 1 |
| (n+1)2-1 |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴Ln=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
点评:本题考查了等差数列的通项公式、等比数列的前n项和公式、“错位相减法”、“裂项求和”,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知定点M(-1,0),N(1,0),P是椭圆
+
=1上动点,则
+
的最小值为( )
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| |PM| |
| 4 |
| |PN| |
| A、2 | ||
B、
| ||
| C、3 | ||
D、3+2
|
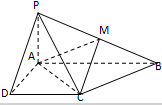 如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=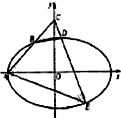 已知B(-1,1)是椭圆
已知B(-1,1)是椭圆