题目内容
11．
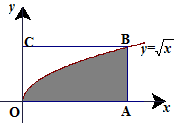如图，长方形的四个顶点为O（0，2），A（4，0），B（4，2），C（0，2），曲线y=$\sqrt{x}$经过点B．现将一质点随机投入长方形OABC中，则质点落在图中阴影区域的概率是$\frac{2}{3}$．
分析 本题考查的知识点是几何概型的意义，关键是要找出图中阴影部分的面积，并将其与长方形面积一块代入几何概型的计算公式进行求解．
解答 解：由已知易得：S长方形=4×2=8，
S阴影=∫04（$\sqrt{x}$）dx=$\frac{2}{3}{x}^{\frac{3}{2}}{|}_{0}^{4}$=$\frac{16}{3}$，故质点落在图中阴影区域的概率P=$\frac{\frac{16}{3}}{8}$=$\frac{2}{3}$，
故答案为$\frac{2}{3}$．
点评 几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．
练习册系列答案
名校课堂系列答案
相关题目
5．已知F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，过F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M，若点M在以线段F1F2为直径的圆上，则该双曲线的离心率为（ ）
| A． | 3 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
2．已知函数$y=sin（2x+\frac{π}{3}-2m）（m＞0）$为偶函数，则m的最小值为（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{3}$ | C． | $\frac{5π}{12}$ | D． | $\frac{7π}{12}$ |
19．等比数列{an}中，an＞0，a5a6=9，则log3a1+log3a2+log3a3+…+log3a10=（ ）
| A． | 12 | B． | 10 | C． | 8 | D． | 2+log35 |
6．
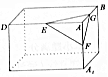如图，用小刀切一块长方体橡皮的一个角，在棱AD、AA1、AB上的截点分别是E、F、G，则截面△EFG（ ）
如图，用小刀切一块长方体橡皮的一个角，在棱AD、AA1、AB上的截点分别是E、F、G，则截面△EFG（ ）| A． | 一定是等边三角形 | B． | 一定是钝角三角形 | ||
| C． | 一定是锐角三角形 | D． | 一定是直角三角形 |
某校从参加考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段后得到如下部分频率分布直方图如图．观察图形的信息，回答下列问题：
3．设函数f（x）=$\frac{{e}^{2}{x}^{2}+1}{x}$，g（x）=$\frac{{e}^{2}x}{{e}^{x}}$，对任意${x_1}，{x_2}∈（{\frac{1}{e}，+∞}）$，不等式$\frac{{g（{x_1}）}}{k}＜\frac{{f（{x_2}）}}{k+2}$恒成立，则正数k的取值范围是（ ）
| A． | （1，+∞） | B． | [1，+∞） | C． | （2，+∞） | D． | [2，+∞） |
20．
已知三棱锥O-ABC，点M，N分别为AB，OC的中点，且$\overrightarrow{OA}$=$\vec a$，$\overrightarrow{OB}$=$\vec b$，$\overrightarrow{OC}$=$\vec c$，用$\vec a$，$\vec b$，$\vec c$表示$\overrightarrow{MN}$，则$\overrightarrow{MN}$等于（ ）
已知三棱锥O-ABC，点M，N分别为AB，OC的中点，且$\overrightarrow{OA}$=$\vec a$，$\overrightarrow{OB}$=$\vec b$，$\overrightarrow{OC}$=$\vec c$，用$\vec a$，$\vec b$，$\vec c$表示$\overrightarrow{MN}$，则$\overrightarrow{MN}$等于（ ）| A． | $\frac{1}{2}（\vec b+\vec c-\vec a）$ | B． | $\frac{1}{2}（\vec a+\vec b-\vec c）$） | C． | $\frac{1}{2}（\vec a-\vec b+\vec c）$ | D． | $\frac{1}{2}（\vec c-\vec a-\vec b）$ |