题目内容
14.函数$f(x)=\frac{x}{{1-{x^2}}}$的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 先求出函数的定义域,再利用函数值,即可判断.
解答 解:由1-x2≠0,解得x≠±1,
∵函数$f(x)=\frac{x}{{1-{x^2}}}$,
当x=2时,f(x)<0,
当x=-2时,f(x)>0,
当x=$\frac{1}{2}$时,f(x)>0,
当x=-$\frac{1}{2}$时,f(x)<0,
故选:B.
点评 本题考查了函数的图象的识别,掌握函数的定义域,函数的值,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.$cos\frac{2π}{3}•tan\frac{7π}{4}$的值为( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
9.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
| A. | y=x3 | B. | y=|x+1| | C. | y=-x2 | D. | y=|x|+1 |
19.设命题p:函数y=cos2x的最小正周期为$\frac{π}{2}$;命题q:函数f(x)=sin(x+$\frac{π}{3}$)的图象的一条对称轴是x=$\frac{π}{6}$对称.则下列判断正确的是( )
| A. | p为真 | B. | ¬q为假 | C. | p∧q为真 | D. | p∨q为假 |
6.用边长为120cm的正方形铁皮做一个无盖水箱,先在四周分别截去一个小正方形,然后把四边翻转90°角,再焊接成水箱,则水箱的最大容积为( )
| A. | 120 000 cm3 | B. | 128 000 cm3 | C. | 150 000 cm3 | D. | 158 000 cm3 |
3.随机抛掷一枚质地均匀的骰子,记正面向上的点数为a,则函数f(x)=x2+2ax+2有两个不同零点的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
4.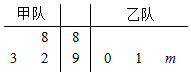 如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
 如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )
如图茎叶图表示的是甲乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m表示,若甲队的平均得分不低于乙队的平均得分,那么m的可能取值集合为( )| A. | {2} | B. | {1,2} | C. | {0,1,2} | D. | {2,3} |
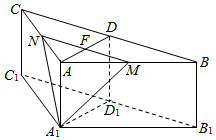 如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N.
如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N.