题目内容
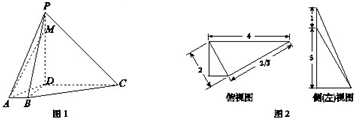
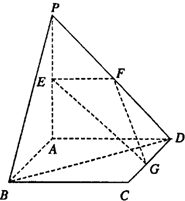 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.(1)求证:PB∥平面EFG;
(2)求异面直线EG与BD所成角的余弦值.
考点:异面直线及其所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)取AB的中点M,连接EM,MG.利用平行四边形的性质、三角形的中位线定理可得MG∥EF.即四点E,F,G,M共面.而在三角形PAB中,再利用三角形的中位线定理可得PB∥EM,利用线面平行的判定定理可得PB∥平面EFGM.
(2)通过建立空间直角坐标系,利用向量的夹角公式即可得出异面直线的夹角.
(2)通过建立空间直角坐标系,利用向量的夹角公式即可得出异面直线的夹角.
解答:
(1)证明:取AB的中点M,连接EM,MG.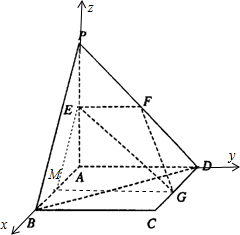
∵MG∥AD,AD∥EF,∴MG∥EF.
∴四点E,F,G,M共面.
而在三角形PAB中,PB∥EM,
又PB?平面EFGM,EM?平面EFGM.
∴PB∥平面EFGM.
即得PB∥平面EFG.
(2)解:如图所示,建立空间直角坐标系.
则B(2,0,0),D(0,2,0),G(1,2,0),E(0,0,1).
∴
=(-2,2,0),
=(1,2,-1).
∴cos<
,
>=
=
=
.
∴异面直线EG与BD所成角的余弦值为
.

∵MG∥AD,AD∥EF,∴MG∥EF.
∴四点E,F,G,M共面.
而在三角形PAB中,PB∥EM,
又PB?平面EFGM,EM?平面EFGM.
∴PB∥平面EFGM.
即得PB∥平面EFG.
(2)解:如图所示,建立空间直角坐标系.
则B(2,0,0),D(0,2,0),G(1,2,0),E(0,0,1).
∴
| BD |
| EG |
∴cos<
| BD |
| EG |
| ||||
|
|
| -2+4 | ||||
|
| ||
| 6 |
∴异面直线EG与BD所成角的余弦值为
| ||
| 6 |
点评:本题考查了平行四边形的性质、三角形的中位线定理、线面平行的判定定理、向量的夹角公式、异面直线的夹角等基础知识与基本技能方法,考查了推理能力和空间想象能力,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
已知一个算法,其流程图如图所示,则输出结果是( )


| A、7 | B、10 | C、13 | D、16 |