题目内容

等差数列{an}和{bn}的前n项和分别为Sn和Tn，已知
a5
b5
=
2
3
，求
S9
T9
．
考点：等差数列的性质
专题：等差数列与等比数列
分析：直接由等差数列的前n项和结合等差数列的性质得到
S9
S9
=
a5
b5
=
2
3
．
解答： 解：在等差数列{an}和{bn}中，
由等差数列的性质可得：
S9=
(a1+a9)×9
2
=9a5，
T9=
(b1+b9)×9
2
=9b5．
又
a5
b5
=
2
3
，
∴
S9
T9
=
9a5
9b5
=
2
3
．
点评：本题考查等差数列的性质，考查了等差数列的前n项和，是基础题．
练习册系列答案
相关题目
函数f（x）=log 
1
2
（a-2x）-（2+x）有零点，则a的取值范围为（　　）
A、（1，+∞）
B、[1，+∞）
C、（-∞，1]
D、（-∞，1）
设数列{an}的前n项和为Sn满足2Sn=an+1-2n+1+1，n∈N*，且a1，a2+5，a3成等差数列．
（1）求a1的值；
（2）求数列{an}的通项公式．
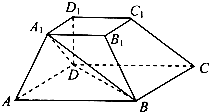如图，在四棱台ABCD-A1B1C1D1中，底面ABCD是平行四边形，DD1⊥平面ABCD，AB=2AD，AD=A1B1，∠BAD=60°．
（1）证明：BD⊥平面ADD1A1；
（2）证明：CC1∥平面A1BD．
已知函数f（x）=lnx，g（x）=（x-a）2+（lnx-a）2．
（Ⅰ）求函数f（x）在A（1，0）处的切线方程；
（Ⅱ）若g′（x）在[1，+∞）上单调递增，求实数a的取值范围；
（Ⅲ）证明：g（x）≥
1
2
．
已知m∈R，命题p：对任意x∈[-1，1]，不等式2x-1≥m2-4m恒成立；命题q：存在 x∈[-1，1]，使得ax≥m成立．
（Ⅰ）若p为真命题，求m的取值范围．
（Ⅱ）当a=2，若p∧q为假，p∨q为真，求m的取值范围．
在△ABC中，角A，B，C所对的边分别为a，b，c，且sin2A+sin2B+cos2C=1+sinAsinB
（1）求角C的大小；
（2）若c=2，且△ABC的面积为
3
，求a，b．
根据要求证明下列各题：
（1）用分析法证明：
3
-
2
＞
6
-
5

（2）用分析法证明：1，
2
，3不可能是一个等差数列中的三项．
已知cosα=-
4
5
，且sinα＞0，tanθ=1，则tan（π-α-θ）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网