题目内容
已知函数f（x）=x3+ax2+bx的图象关于点（1，1）对称，给出下列命题：
①f（x）在R上单调递增；
②f（x）在R上有极值；
③函数y=f（x+1）-1是奇函数；
④函数y=f（x）-x必有三个零点．则其中假命题的序号是 ．
①f（x）在R上单调递增；
②f（x）在R上有极值；
③函数y=f（x+1）-1是奇函数；
④函数y=f（x）-x必有三个零点．则其中假命题的序号是
考点：利用导数研究函数的单调性,利用导数研究函数的极值
专题：导数的综合应用
分析：利用图象的对称性解得a、b的值，利用导数判断函数的单调性及极值，得出①正确，②错误；
根据函数奇偶性的定义判断③正确，根据二次函数根的判断可得④错误．
根据函数奇偶性的定义判断③正确，根据二次函数根的判断可得④错误．
解答：
解：∵f（x）=x3+ax2+bx的图象关于点（1，1）对称，
∴2-f（x）=（2-x）3+a（2-x）2+b（2-x），
即f（x）=x3-（a+6）x2+（b+4a+12）x-4a-2b，
比较系数得
解得
∴f（x）=x3-3x2+6x，
∴f′（x）=3x2-6x+6=3（x-1）2+3＞0，f（x）在R上单调递增，故①正确，②错误；
由y=f（x+1）-1=x3+3x+3得y=f（x+1）-1是奇函数，故③正确，
由y=f（x）-x=x（x2-3x+5）得，令g（x）=x2-3x+5则△=9-20=-11＜0，
∴x（x2-3x+5）=0有且只有一解x=0，故④错误．
故答案为②④．
∴2-f（x）=（2-x）3+a（2-x）2+b（2-x），
即f（x）=x3-（a+6）x2+（b+4a+12）x-4a-2b，
比较系数得
|
|
∴f（x）=x3-3x2+6x，
∴f′（x）=3x2-6x+6=3（x-1）2+3＞0，f（x）在R上单调递增，故①正确，②错误；
由y=f（x+1）-1=x3+3x+3得y=f（x+1）-1是奇函数，故③正确，
由y=f（x）-x=x（x2-3x+5）得，令g（x）=x2-3x+5则△=9-20=-11＜0，
∴x（x2-3x+5）=0有且只有一解x=0，故④错误．
故答案为②④．
点评：本题主要考查函数的对称性、单调性、极值、奇偶性、零点的判断方法，是对函数性质的综合考查，属中档题．
练习册系列答案
相关题目
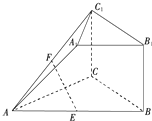如图所示的几何体中，四边形BB1C1C是矩形，BB1⊥平面ABC，CA=CB，A1B1∥AB，AB=2A1B1，E，F分别是AB，AC1的中点．
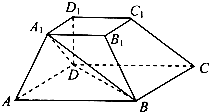如图，在四棱台ABCD-A1B1C1D1中，底面ABCD是平行四边形，DD1⊥平面ABCD，AB=2AD，AD=A1B1，∠BAD=60°．