题目内容
某中学有有教师300人,其中高级、中级、初级职称教师人数之比为1:3:2,现在准备用分层抽样法抽取72人的工资作样本,那么应从初级教师中抽( )个人的工资.
| A、12 | B、18. | C、24 | D、36 |
考点:分层抽样方法
专题:计算题,概率与统计
分析:求出初级教师的比例,然后根据分层抽样的定义,即可得到结论.
解答:
解:∵高级、中级、初级职称教师人数之比为1:3:2,
∴初级教师的比例为
=
,
∴应从初级教师中抽72×
=24个人的工资.
故选:C.
∴初级教师的比例为
| 2 |
| 1+3+2 |
| 1 |
| 3 |
∴应从初级教师中抽72×
| 1 |
| 3 |
故选:C.
点评:本题主要考查分层抽样的应用,利用分层抽样的定义是解决本题的关键,比较基础.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
函数f(x)=ax2+bx+5满足条件f(-1)=f(3),则f(2)的值为( )
| A、5 | B、6 |
| C、8 | D、与a,b的值有关 |
已知tanα=
,则cos2α的值为( )
| 1 |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
设a=log
3,b=(
)0.2,c=2
,则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、a<c<b |
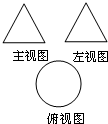 (文科)一个几何体的三视图如图所示,其中主视图和左视图是全等的正三角形,且该几何体的表面积为3π,则该几何体的体积为
(文科)一个几何体的三视图如图所示,其中主视图和左视图是全等的正三角形,且该几何体的表面积为3π,则该几何体的体积为 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=210,则i、j的值分别为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8.若ai,j=210,则i、j的值分别为