题目内容
已知tanα=
,则cos2α的值为( )
| 1 |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点:二倍角的余弦,同角三角函数基本关系的运用
专题:三角函数的求值
分析:利用余弦的二倍角公式可求得cos2α=cos2α-sin2α,进而利用同角三角基本关系,使其除以sin2α+cos2α,分子分母同时除以cos2a,转化成正切,然后把tanα的值代入即可.
解答:
解:cos2α=cos2α-sin2α=
=
=
=
.
故选:D.
| cos2α-sin2α |
| cos2α+sin2α |
| 1-tan2α |
| 1+tan2α |
1-
| ||
1+
|
| 3 |
| 5 |
故选:D.
点评:本题主要考查了同角三角函数的基本关系和二倍角的余弦函数的公式.解题的关键是利用同角三角函数中的平方关系,完成了弦切的互化.

练习册系列答案
相关题目
定义在R上的偶函数f (x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有
<0,又f (-3)=1,则不等式f (x)<1的解集为( )
| f(x2)-f(x1) |
| x2-x1 |
| A、{x|x<-3或x>3} |
| B、{x|x<-3或0<x<3} |
| C、{x|x>3或-3<x<0} |
| D、{x|-3<x<0或0<x<3} |
已知a=(
)0.3,b=0.3-2,c=log
2,则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、a>b>c |
| B、a>c>b |
| C、b>a>c |
| D、c>b>a |
下列函数与y=x有相同图象的一个函数是( )
A、y=
| ||
B、y=
| ||
| C、y=logaax | ||
| D、y=a logax(a>0且a≠1) |
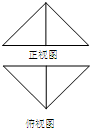 把边长为1的正方形ABCD沿对角线BD折起,连结AC,得到三棱锥C-ABD,其正视图与俯视图均为全等的等腰直角三角形,如图所示,则侧视图的面积为( )
把边长为1的正方形ABCD沿对角线BD折起,连结AC,得到三棱锥C-ABD,其正视图与俯视图均为全等的等腰直角三角形,如图所示,则侧视图的面积为( )