题目内容
已知直线l经过两直线x-y+1=0和2x+3y-8=0的交点，且经过点P（4，-2），求直线l的方程．
考点：直线的两点式方程,两条直线的交点坐标
专题：直线与圆
分析：法一：求出直线的交点，再利用两点式即可得出；
法二：利用直线系即可得出．
法二：利用直线系即可得出．
解答：
解：（法一）联立方程组
，解得
，
∴直线x-y+1=0和2x+3y-8=0的交点坐标为A（1，2）．
∵直线l经过点A（1，2）和点P（4，-2）
由两点式得直线l的方程为：
=
．
化简得直线l的方程为：4x+3y-10=0…（12分）
（法二）依题意，设直线l的方程为：x-y+1+λ（2x+3y-8）=0，
整理，得 （2λ+1）x+（3λ-1）y+1-8λ=0，
∵直线l经过点P（4，-2），
将
代入（2λ+1）x+（3λ-1）y+1-8λ=0，
得4×（2λ+1）-2×（3λ-1）+1-8λ=0，
解得λ=
，
∴直线l的方程为：x-y+1+
×(2x+3y-8)=0
即4x+3y-10=0．…（12分）
|
|
∴直线x-y+1=0和2x+3y-8=0的交点坐标为A（1，2）．
∵直线l经过点A（1，2）和点P（4，-2）
由两点式得直线l的方程为：
| y-2 |
| -2-2 |
| x-1 |
| 4-1 |
化简得直线l的方程为：4x+3y-10=0…（12分）
（法二）依题意，设直线l的方程为：x-y+1+λ（2x+3y-8）=0，
整理，得 （2λ+1）x+（3λ-1）y+1-8λ=0，
∵直线l经过点P（4，-2），
将
|
得4×（2λ+1）-2×（3λ-1）+1-8λ=0，
解得λ=
| 7 |
| 6 |
∴直线l的方程为：x-y+1+
| 7 |
| 6 |
即4x+3y-10=0．…（12分）
点评：本题考查了直线的交点、两点式、直线系，属于基础题．
练习册系列答案
学业测评一课一测系列答案
相关题目
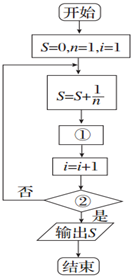如图给出的是计算1+| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 9 |
| A、n=n+2，i＞5？ |
| B、n=n+2，i=5？ |
| C、n=n+1，i=5？ |
| D、n=n+1，i＞5？ |
已知?的ABCD顶点A，B，C的坐标分别为（-2，1），（-1，3），（3，4），则顶点D的坐标为（ ）
| A、（4，6） |
| B、（2，2） |
| C、（0，0） |
| D、（0，4） |
已知f（x）是偶函数，且在（-∞，0]上是增函数．若f（lnx）＜f（1），则x的取值范围是（ ）
| A、（e，+∞） | ||
B、(
| ||
C、(e，+∞)∪(0，
| ||
D、(
|
若a=20.2，b=log4（3.2），c=log2（0.5），则（ ）
| A、a＞b＞c |
| B、b＞a＞c |
| C、c＞a＞b |
| D、b＞c＞a |