��Ŀ����
10����֪$\overrightarrow{AB}=3\overrightarrow e��\overrightarrow{CD}=-5\overrightarrow e��\overrightarrow e��\overrightarrow 0��$����$|{\overrightarrow{AD}}|=|{\overrightarrow{BC}}|$�����ı���ABCD�ǣ�������| A�� | ƽ���ı��� | B�� | ���� | C�� | �������� | D�� | ���� |
���� �����������߶��������εĶ��弴���жϳ����ۣ�
��� �⣺��$\overrightarrow{AB}=3\overrightarrow e��\overrightarrow{CD}=-5\overrightarrow e��\overrightarrow e��\overrightarrow 0��$����$\overrightarrow{AB}$=-$\frac{3}{5}$$\overrightarrow{CD}$��
��$|{\overrightarrow{AD}}|=|{\overrightarrow{BC}}|$�����ı���ABCD�ǵ������Σ�
��ѡ��C��
���� ���⿼�����������߶��������εĶ��壬����������������������������ڻ����⣮

��ϰ��ϵ�д�
�����Ŀ
1��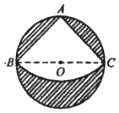 ��ͼ����һֱ��Ϊ40cm��Բ����Ƥ��Ҫ���м���һ������Բ�Ľ�Ϊ900��������ƤABC���Ѽ���������Χ��һ��Բ����ô��Բ�ĸ�Ϊ��������
��ͼ����һֱ��Ϊ40cm��Բ����Ƥ��Ҫ���м���һ������Բ�Ľ�Ϊ900��������ƤABC���Ѽ���������Χ��һ��Բ����ô��Բ�ĸ�Ϊ��������
 ��ͼ����һֱ��Ϊ40cm��Բ����Ƥ��Ҫ���м���һ������Բ�Ľ�Ϊ900��������ƤABC���Ѽ���������Χ��һ��Բ����ô��Բ�ĸ�Ϊ��������
��ͼ����һֱ��Ϊ40cm��Բ����Ƥ��Ҫ���м���һ������Բ�Ľ�Ϊ900��������ƤABC���Ѽ���������Χ��һ��Բ����ô��Բ�ĸ�Ϊ��������| A�� | $5\sqrt{2}cm$ | B�� | 20cm | C�� | $10\sqrt{7}cm$ | D�� | $5\sqrt{30}cm$ |
18�����DZ�ȥ�����ԭ�ĵ�·��6�����������ԭȥ���ĵ�·��20�����DZ�����屻�����ԭ����������ȥ���IJ�ͬ�߷��У�������
| A�� | 120 | B�� | 26 | C�� | 20 | D�� | 6 |
5��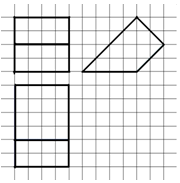 ��ͼ��������С�����εı߳�Ϊ$\frac{1}{2}$������������ij�ռ伸���������ͼ����ü���������Ϊ��������
��ͼ��������С�����εı߳�Ϊ$\frac{1}{2}$������������ij�ռ伸���������ͼ����ü���������Ϊ��������
 ��ͼ��������С�����εı߳�Ϊ$\frac{1}{2}$������������ij�ռ伸���������ͼ����ü���������Ϊ��������
��ͼ��������С�����εı߳�Ϊ$\frac{1}{2}$������������ij�ռ伸���������ͼ����ü���������Ϊ��������| A�� | 24 | B�� | 12 | C�� | 4 | D�� | 6 |
15����AΪ��ABC���ڽǣ������к�����һ��ȡ��ֵ���ǣ�������
| A�� | cosA | B�� | sinA | C�� | tanA | D�� | sin2A |
2����֪������x���ϣ������߷���Ϊ$y=��\frac{3}{4}x$��˫���ߺ�����$\frac{x^2}{4}+\frac{y^2}{b^2}=1��{b��0}��$��������֮��Ϊ1����b��ֵ Ϊ��������
| A�� | $\frac{6}{5}$ | B�� | 3 | C�� | 3��4 | D�� | $\frac{6}{5}$��$\frac{10}{3}$ |
20�����к����в����溯�����ǣ�������
| A�� | $y=\frac{{��{{a^x}+1}��x}}{{{a^x}-1}}��{a��0��a��1}��$ | B�� | $y=\frac{{{a^x}-{a^{-x}}}}{2}��{a��0��a��1}��$ | ||
| C�� | $y=\left\{\begin{array}{l}1����{x��0}��\\-1����{x��0}��\end{array}\right.$ | D�� | $y={log_a}\frac{1+x}{1-x}��{a��0��a��1}��$ |