题目内容
已知各项均为正数的数列{an}前n项和Sn满足S1>1,且6Sn=(an+1)(an+2),(n∈N*)
(1)求通项an;
(2)设bn=|
-3n+20|,求数列{bn}前n项和Tn的表达式.
(1)求通项an;
(2)设bn=|
| Sn |
| n |
考点:数列递推式,数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)先根据题设求得a1,进而根据an+1=Sn+1-Sn整理得(an+1+an)(an+1-an-3)=0,求得an+1-an=3,判断出{an}是公差为3,首项为2的等差数列,则数列的通项公式可得;
(2)由(1)求出数列{an}前n项和Sn,代入
-3n+20,然后分段求出数列{bn}前n项和Tn.
(2)由(1)求出数列{an}前n项和Sn,代入
| Sn |
| n |
解答:
解:(1)由a1=S1=
(a1+1)(a2+1),
解得a1=1或a1=2,
由假设a1=S1>1,因此a1=2,
又由an+1=Sn+1-Sn=
(an+1+1)(an+1+2)-
(an+1)(an+2),
得(an+1+an)(an+1-an-3)=0,
即an+1-an-3=0或an+1=-an,
∵an>0,
故an+1=-an不成立,舍去,
因此an+1-an=3,
从而{an}是公差为3,首项为2的等差数列,
故{an}的通项为an=3n-1;
(2)由(1)得,Sn=na1+
d=2n+
n(n-1)=
n2+
n,
∴
-3n+20=
n+
-3n+20=-
n+
.
由-
n+
>0,得n<
,
∴数列{-
n+
}的前13项大于0,自14项起小于0.
又数列{-
n+
}的首项为19,公差为-
.
∴当n≤13时,数列bn的前n项和Tn=19n+
×(-
)=-
n2+
n.
当n>13时,Tn=
n2-
n+2(-
×132+
×13)=
n2-
n+260.
∴Tn=
.
| 1 |
| 6 |
解得a1=1或a1=2,
由假设a1=S1>1,因此a1=2,
又由an+1=Sn+1-Sn=
| 1 |
| 6 |
| 1 |
| 6 |
得(an+1+an)(an+1-an-3)=0,
即an+1-an-3=0或an+1=-an,
∵an>0,
故an+1=-an不成立,舍去,
因此an+1-an=3,
从而{an}是公差为3,首项为2的等差数列,
故{an}的通项为an=3n-1;
(2)由(1)得,Sn=na1+
| n(n-1) |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴
| Sn |
| n |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 41 |
| 2 |
由-
| 3 |
| 2 |
| 41 |
| 2 |
| 41 |
| 3 |
∴数列{-
| 3 |
| 2 |
| 41 |
| 2 |
又数列{-
| 3 |
| 2 |
| 41 |
| 2 |
| 3 |
| 2 |
∴当n≤13时,数列bn的前n项和Tn=19n+
| n(n-1) |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 79 |
| 4 |
当n>13时,Tn=
| 3 |
| 4 |
| 79 |
| 4 |
| 3 |
| 4 |
| 79 |
| 4 |
| 3 |
| 4 |
| 79 |
| 4 |
∴Tn=
|
点评:本题考查了数列递推式,考查了等差关系的确定,训练了等差数列前n项和的求法,体现了分类讨论的数学思想方法,是中档题.

练习册系列答案
相关题目

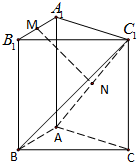 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是A1B1,AC1的中点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是A1B1,AC1的中点.