题目内容
已知矩阵M=
的一个特征值为-1，则其另一个特征值为 ．
|
考点：特征值与特征向量的计算
专题：选作题,矩阵和变换
分析：根据矩阵M的一个特征值为-1，代入特征多项式求出x的值，从而求出矩阵M的另一个特征值．
解答：
解：矩阵M的特征多项式f（λ）=
=（λ-1）（λ-1）+2x，
又∵矩阵M的一个特征值为-1，
∴f（-1）=0，∴x=-2，
由f（λ）=（λ-1）2-4=0，得λ1=-1，λ2=3，
∴矩阵M的另一个特征值为3．
故答案为：3．
|
又∵矩阵M的一个特征值为-1，
∴f（-1）=0，∴x=-2，
由f（λ）=（λ-1）2-4=0，得λ1=-1，λ2=3，
∴矩阵M的另一个特征值为3．
故答案为：3．
点评：本题主要考查矩阵的特征值与特征向量等基础知识，考查运算求解能力及函数与方程思想，属于基础题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
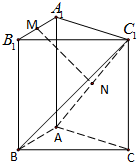三棱柱ABC-A1B1C1中，侧棱与底面垂直，∠ABC=90°，AB=BC=BB1=2，M，N分别是A1B1，AC1的中点．