题目内容
已知f(x)=-
+sin(
-2x)+cos(2x-
)+cos2x.
(1)求f(x)的最小正周期;
(2)求f(x)在区间[-
,
]上的最大值,并求出f(x)取最大值时x的值.
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
(1)求f(x)的最小正周期;
(2)求f(x)在区间[-
| π |
| 8 |
| 3π |
| 8 |
考点:三角函数中的恒等变换应用,复合三角函数的单调性
专题:三角函数的图像与性质
分析:(1)利用两角和公式和二倍角公式对函数解析式进行化简,利用周期公式求得函数的最小正周期.
(2)根据x的范围,确定2x的范围,进而根据三角函数的图象求得函数的最大值.
(2)根据x的范围,确定2x的范围,进而根据三角函数的图象求得函数的最大值.
解答:
解:f(x)=-
+sin(
-2x)+cos(2x-
)+cos2x=cos(2x+
)+cos(2x-
)+
-
=2cos2xcos
+
=
cos2x,
故f(x)的周期是T=
=π.
(2)∵x∈[-
,
],2x∈[-
,
],故当x=0时,f(x)的最大值是
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| cos2x |
| 2 |
| 3 |
| 2 |
故f(x)的周期是T=
| 2π |
| 2 |
(2)∵x∈[-
| π |
| 8 |
| 3π |
| 8 |
| π |
| 4 |
| 3π |
| 4 |
| 3 |
| 2 |
点评:本题主要考查了三角函数图象与性质,三角函数恒等变换的应用.考查了学生对三角函数基础知识的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
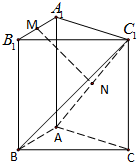 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是A1B1,AC1的中点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是A1B1,AC1的中点.