题目内容
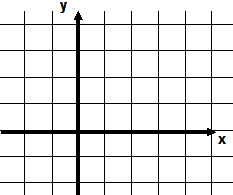
在平面直角坐标系xOy中,圆C:(x-2)2+(y-b)2=r2经过点(1,0),且圆C被x轴和y轴截得的弦长之比为1:
,求圆的方程.
| 6 |
考点:直线与圆相交的性质
专题:直线与圆
分析:直接利用已知条件点在圆上,以及圆C被x轴和y轴截得的弦长之比为1:
,列出方程组求出b、r,即可得到圆的方程.
| 6 |
解答:
解:∵圆C:(x-2)2+(y-b)2=r2经过点(1,0),
∴b2=r2-1,…①.
y=0时,(x-2)2+b2=r2,解得|x2-x1|=2
.
x=0时,4+(y-b)2=r2,|y2-y1|=2
,
圆C被x轴和y轴截得的弦长之比为1:
,
∴
=
…②,
解①②可得r=
,b=±3.
圆的方程::(x-2)2+(y±3)2=10.
∴b2=r2-1,…①.
y=0时,(x-2)2+b2=r2,解得|x2-x1|=2
| r2-b2 |
x=0时,4+(y-b)2=r2,|y2-y1|=2
| r2-4 |
圆C被x轴和y轴截得的弦长之比为1:
| 6 |
∴
2
| ||
2
|
| 1 | ||
|
解①②可得r=
| 10 |
圆的方程::(x-2)2+(y±3)2=10.
点评:本题考查直线与圆的位置关系,圆的标准方程的求法,考查计算能力.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
(x-
y)8的展开式中x6y2项的系数是( )
| 2 |
| A、56 | B、-56 |
| C、28 | D、-28 |
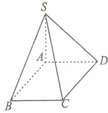 如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥平面ABCD
如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA⊥平面ABCD