题目内容
1.f(x)=sinx•cosx+$\sqrt{3}$sin2x的单调递减区间为[$\frac{5π}{12}$+kπ,$\frac{11π}{12}$+kπ],k∈Z.分析 利用三角恒等变换化简f(x)为正弦型函数,根据正弦函数的单调性写出f(x)的单调递减区间.
解答 解:f(x)=sinx•cosx+$\sqrt{3}$sin2x
=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$(1-cos2x)
=sin(2x-$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$,
令$\frac{π}{2}$+2kπ≤2x-$\frac{π}{3}$≤$\frac{3π}{2}$+2kπ,k∈Z,
∴$\frac{5π}{6}$+2kπ≤2x≤$\frac{11π}{6}$+2kπ,k∈Z,
即$\frac{5π}{12}$+kπ≤x≤$\frac{11π}{12}$+kπ,k∈Z,
∴f(x)的单调递减区间为[$\frac{5π}{12}$+kπ,$\frac{11π}{12}$+kπ],k∈Z.
故答案为:[$\frac{5π}{12}$+kπ,$\frac{11π}{12}$+kπ],k∈Z.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了三角恒等变换问题,是基础题目.

练习册系列答案
相关题目
1.若集合A={x|(x+4)(x+1)<0},集合B={x|x<-2},则A∩(∁RB)等于( )
| A. | (-2,-1) | B. | [-2,4) | C. | [-2,-1) | D. | ∅ |
9.有下列命题:(1)若z是复数,则|z|2=z2;(2)任意两个复数不能比较大小;(3)b2-4ac>0时,一元二次方程ax2+bx+c=0(a,b,c∈C)有两个不等的实数根,其中所有错误命题的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
16.直线a,b,c及平面α,β,γ,下列命题正确的是( )
| A. | 若a?α,b?α,c⊥a,c⊥b 则c⊥α | B. | 若a⊥α,b⊥α 则a∥b | ||
| C. | 若a∥α,α∩β=b 则a∥b | D. | 若b?α,a∥b 则 a∥α |
13.已知f(x)=ax3+bx+5,其中a,b为常数,若f(-9)=-7,则f(9)=( )
| A. | 17 | B. | 7 | C. | 16 | D. | 8 |
10.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则该三棱锥S-ABC的外接球的表面积为( )
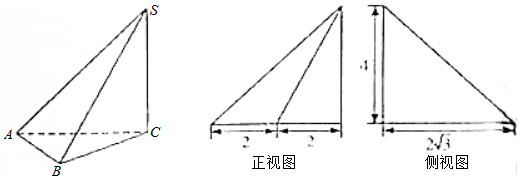

| A. | 32π | B. | $\frac{112π}{3}$ | C. | $\frac{28π}{3}$ | D. | $\frac{64}{3}$π |