题目内容
11.若x,y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x-2≤0\\ x+y-2≥0\end{array}\right.$,则$z=\frac{y}{x}$的最大值为3.分析 由约束条件作出可行域,再由$z=\frac{y}{x}$的几何意义,即可行域内的动点与原点连线的斜率求解.
解答 解:由约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x-2≤0\\ x+y-2≥0\end{array}\right.$作出可行域如图,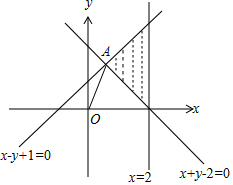
联立$\left\{\begin{array}{l}{x-y+1=0}\\{x+y-2=0}\end{array}\right.$,解得A($\frac{1}{2}$,$\frac{3}{2}$).
$z=\frac{y}{x}$的几何意义为可行域内的动点与原点连线的斜率,
则$z=\frac{y}{x}$的最大值为$\frac{\frac{3}{2}}{\frac{1}{2}}=3$.
故答案为:3.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
19.在长方体ABCD-A1B1C1D1中,AB=1,BC=3,AA1=2,E,F分别是下底面的棱A1B1,B1C1的中点,M是上底面的棱AD上一点,且AM=2,过M,E,F的平面与BA的延长线交于点N,则MN的长度为( )
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{10}}}{3}$ | C. | $\frac{{\sqrt{10}}}{2}$ | D. | $\frac{{2\sqrt{10}}}{3}$ |
16.已知向量$\overrightarrow a=({1,-2}),\overrightarrow b=({k,4})$,且$\overrightarrow a∥\overrightarrow b$,则实数k的值为( )
| A. | -2 | B. | 2 | C. | 8 | D. | -8 |
20.已知圆C:(x-$\sqrt{3}$)2+(y-1)2=1和两点A(-t,0),B(t,0)(t>0),若圆C上存在点P,使得∠APB=90°,则t的取值范围是( )
| A. | (0,2] | B. | [1,2] | C. | [2,3] | D. | [1,3] |