题目内容
20.在1,2,3,4四个数中随机地抽取一个数记为a,再在剩余的三个数中随机地抽取一个数记为b,则“$\frac{a}{b}$不是整数”的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 先求出基本事件总数,再求出“$\frac{a}{b}$不是整数”包含的基本事件个数,由此能求出“$\frac{a}{b}$不是整数”的概率.
解答 解:∵在1,2,3,4四个数中随机地抽取一个数记为a,
再在剩余的三个数中随机地抽取一个数记为b,
∴基本事件总数n=4×3=12,
“$\frac{a}{b}$不是整数”包含的基本事件有$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,$\frac{2}{3}$,$\frac{2}{4}$,$\frac{3}{4}$,$\frac{3}{2}$,$\frac{4}{3}$,共8个,
∴“$\frac{a}{b}$不是整数”的概率p=$\frac{m}{n}$=$\frac{8}{12}=\frac{2}{3}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.将y=sin2x+cos2x的图象向右平移$\frac{π}{4}$个单位后,所得图象的解析式是( )
| A. | y=sin2x-cos2x | B. | y=cos2x-sin2x | C. | y=cos2x+sin2x | D. | y=cosxsinx |
5.已知集合M={0,i}(i是虚数单位),集合N={x|x2+1=0,x∈C},则集合M∪N=( )
| A. | i | B. | {i} | C. | {0,i} | D. | {-i,0,i} |
12.命题“?a∈R,函数y=π”是增函数的否定是( )
| A. | “?a∈R,函数y=π”是减函数 | B. | “?a∈R,函数y=π”不是增函数 | ||
| C. | “?a∈R,函数y=π”不是增函数 | D. | “?a∈R,函数y=π”是减函数 |
9.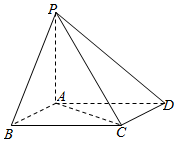 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ≤$\frac{π}{2}$),则四棱锥P-ABCD的体积V的取值范围是( )
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ≤$\frac{π}{2}$),则四棱锥P-ABCD的体积V的取值范围是( )
 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ≤$\frac{π}{2}$),则四棱锥P-ABCD的体积V的取值范围是( )
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ≤$\frac{π}{2}$),则四棱锥P-ABCD的体积V的取值范围是( )| A. | [$\frac{\sqrt{2}}{6}$,$\frac{1}{3}$) | B. | ($\frac{\sqrt{2}}{12}$,$\frac{1}{6}$] | C. | ($\frac{\sqrt{2}}{6}$,$\frac{1}{3}$] | D. | [$\frac{\sqrt{2}}{12}$,$\frac{1}{6}$) |
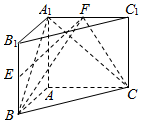 如图,直三棱柱ABC-A1B1C1中,AB⊥AC,E,F分别是BB1,A1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,E,F分别是BB1,A1C1的中点.