题目内容
15.已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,左顶点为A,上顶点为E,O是坐标原点,△OAE面积为$\sqrt{3}$.(1)求椭圆G的方程;
(2)若过椭圆G的右焦点作垂直于x轴的直线m与G在第一象限内交于点M,平行于AM的直线l与椭圆G相交于B,C两点,判断直线MB,MC是否关于直线m对称,并说明理由.
分析 (1)运用椭圆的离心率公式和实际行动面积公式,及a,b,c的关系,解得a,b,进而得到椭圆方程;
(2)求得椭圆的右焦点坐标,M,A的坐标,求得斜率.可设BC的方程为y=$\frac{1}{2}$x+t,代入椭圆方程3x2+4y2=12,
可得x2+tx+t2-3=0,设B(x1,y1),C(x2,y2),运用韦达定理和直线的斜率公式,可得kMB+kMC=0,进而得到直线MB和直线MC关于直线m对称.
解答 解:(1)由题意可得e=$\frac{c}{a}$=$\frac{1}{2}$,
由A(-a,0),E(0,b),
可得△OAE面积为$\sqrt{3}$,
即有$\frac{1}{2}$ab=$\sqrt{3}$,
又a2-b2=c2,
解得a=2,b=$\sqrt{3}$,c=1,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)椭圆的右焦点为(1,0),
可得M(1,$\frac{3}{2}$),A(-2,0),kAM=$\frac{\frac{3}{2}-0}{1+2}$=$\frac{1}{2}$,
设BC的方程为y=$\frac{1}{2}$x+t,代入椭圆方程3x2+4y2=12,
可得x2+tx+t2-3=0,
设B(x1,y1),C(x2,y2),
即有x1+x2=-t,x1x2=t2-3,
由kMB+kMC=$\frac{{y}_{1}-\frac{3}{2}}{{x}_{1}-1}$+$\frac{{y}_{2}-\frac{3}{2}}{{x}_{2}-1}$=$\frac{\frac{1}{2}{x}_{1}+t-\frac{3}{2}}{{x}_{1}-1}$+$\frac{\frac{1}{2}{x}_{2}+t-\frac{3}{2}}{{x}_{2}-1}$
=$\frac{{x}_{1}{x}_{2}-2t+3+(t-2)({x}_{1}+{x}_{2})}{({x}_{1}-1)({x}_{2}-1)}$=$\frac{{t}^{2}-3-2t+3-{t}^{2}+2t}{({x}_{1}-1)({x}_{2}-1)}$=0.
即有直线MB和直线MC关于直线m对称.
点评 本题考查椭圆的方程的求法,注意运用离心率公式,考查直线和椭圆方程联立,运用韦达定理和直线的斜率公式,化简整理,考查运算能力,属于中档题.

| A. | i | B. | {i} | C. | {0,i} | D. | {-i,0,i} |
| A. | [2,+∞) | B. | [1,2] | C. | [1,+∞) | D. | (0,2] |
| A. | p是真命题且q是假命题 | B. | p是真命题且q是真命题 | ||
| C. | p是假命题且q是真命题 | D. | p是真命题且q是假命题 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
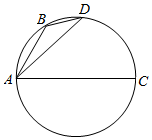 如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )