题目内容
 如图,△ABC在平面α内,∠ACB=90°,AB=2BC=2,P为平面α外一个动点,且PC=
如图,△ABC在平面α内,∠ACB=90°,AB=2BC=2,P为平面α外一个动点,且PC=| 3 |
(Ⅰ)问当PA的长为多少时,AC⊥PB.
(Ⅱ)当△PAB的面积取得最大值时,求直线BC与平面PAB所成角的大小.
考点:直线与平面所成的角
专题:空间角
分析:(Ⅰ)由已知条件推导出AC⊥BC,当AC⊥PC时,AC⊥PB,由此能求出当PA=
时,AC⊥PB.
(Ⅱ)由已知条件推导出当△PAB的面积取得最大值时,∠PBA=90°,从而能求出∠CBD就是直线BC与平面PAB所成角,由此能求出直线BC与平面PAB所成角的大小.
| 6 |
(Ⅱ)由已知条件推导出当△PAB的面积取得最大值时,∠PBA=90°,从而能求出∠CBD就是直线BC与平面PAB所成角,由此能求出直线BC与平面PAB所成角的大小.
解答:
解:(Ⅰ)∵∠ACB=90°,∴AC⊥BC,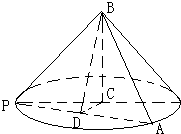
当AC⊥PC时,AC⊥平面PBC,而PB?平面PBC,∴AC⊥PB,
此时,PA=
=
=
,
即当PA=
时,AC⊥PB.
(Ⅱ)在△PBC中,∵PC=
,∠PBC=60°,BC=1,
∴BC⊥PC,当△PAB的面积取得最大值时,∠PBA=90°,
如图,在Rt△PBA中,∵AB=PB=2,∴BD=
,
又在Rt△BCD中,∵BC=1,∴CD=1,
∵PA⊥平面BCD,∴平面BCD⊥平面PBA,
∴∠CBD就是直线BC与平面PAB所成角,
在Rt△BCD中,∵BC=CD=1,∴∠CBD=45°,
∴直线BC与平面PAB所成角的大小为45°.

当AC⊥PC时,AC⊥平面PBC,而PB?平面PBC,∴AC⊥PB,
此时,PA=
| AC2+PC2 |
| 3+3 |
| 6 |
即当PA=
| 6 |
(Ⅱ)在△PBC中,∵PC=
| 3 |
∴BC⊥PC,当△PAB的面积取得最大值时,∠PBA=90°,
如图,在Rt△PBA中,∵AB=PB=2,∴BD=
| 2 |
又在Rt△BCD中,∵BC=1,∴CD=1,
∵PA⊥平面BCD,∴平面BCD⊥平面PBA,
∴∠CBD就是直线BC与平面PAB所成角,
在Rt△BCD中,∵BC=CD=1,∴∠CBD=45°,
∴直线BC与平面PAB所成角的大小为45°.
点评:本题考查异面直线垂直的条件的判断,考查直线与平面所成角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
执行如图所示的程序框图,如果输出的结果为
,则判断框内应填入的条件是( )
| 15 |
| 8 |

| A、k<3 | B、k>3 |
| C、k<4 | D、k>4 |
某四棱锥的三视图如图所示,则最长的一条侧棱长度为( )


A、
| ||
B、
| ||
C、
| ||
D、
|