Question

14．设D为△ABC所在平面内一点，$\overrightarrow{BC}$=4$\overrightarrow{CD}$，则（　　）

• A． $\overrightarrow{AD}$=-$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{4}{3}$$\overrightarrow{AC}$
• B． $\overrightarrow{AD}$=-$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{5}{4}$$\overrightarrow{AC}$
• C． $\overrightarrow{AD}$=$\frac{1}{5}$$\overrightarrow{AB}$+$\frac{4}{5}$$\overrightarrow{AC}$
• D． $\overrightarrow{AD}$=$\frac{4}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$

Answer 1

分析 利用向量三角形法则、向量共线定理即可得出．

解答 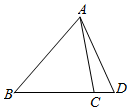解：$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{AB}$+$\overrightarrow{BC}+\overrightarrow{CD}$=$\overrightarrow{AB}$+$\frac{5}{4}$$\overrightarrow{BC}$=$\overrightarrow{AB}$+$\frac{5}{4}（\overrightarrow{AC}-\overrightarrow{AB}）$=-$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{5}{4}$$\overrightarrow{AC}$．
故选：B．

点评 本题考查了向量三角形法则、向量共线定理，考查了推理能力与计算能力，属于基础题．