题目内容
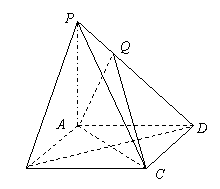
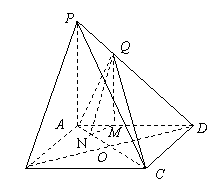
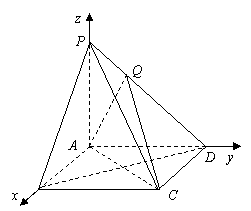
如图,棱锥 的底面
的底面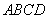 是矩形,
是矩形,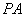 ⊥平面
⊥平面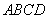 ,
,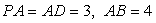 ,
,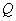 为棱
为棱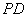 上一点,且
上一点,且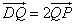 .
.
(Ⅰ)求二面角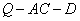 的余弦值;
的余弦值;
(Ⅱ)求点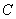 到平面
到平面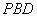 的距离.
的距离.
 |
解法一:
(Ⅰ)在棱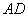 取三等分点
取三等分点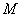 ,使
,使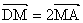 ,则
,则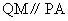 ,
,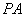 ⊥平面
⊥平面 ,
,
 ⊥平面
⊥平面 ,过点
,过点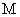 作
作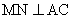 于
于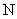 ,连结
,连结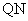 ,
,
则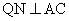 ,
,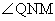 为所求二面角
为所求二面角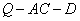 的平面角.
的平面角.
在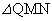 中,
中, ,
,
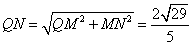 ,
,
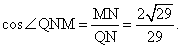
所以,二面角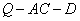 的余弦值为
的余弦值为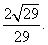
 (Ⅱ)因为
(Ⅱ)因为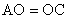 ,所以点
,所以点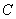 到平面
到平面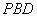 的距离等于
的距离等于
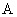 到平面
到平面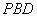 的距离,
的距离,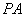 ⊥平面
⊥平面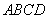 ,
,
过点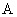 作
作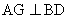 于
于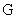 ,连结
,连结 ,则
,则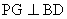 ,
,
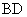 ⊥平面
⊥平面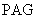 ,过点
,过点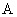 作
作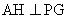 于
于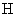 ,
,
则 ,
, 为所求距离,
为所求距离,
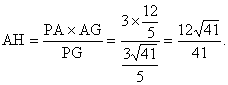
 所以,求点
所以,求点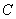 到平面
到平面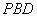 的距离为
的距离为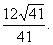
解法二:
证:(Ⅰ)建立如图所示的直角坐标系,
则A(0,0,0)、D(0,3,0)、P(0,0,3)、
B(4,0,0)、C(4,3,0), 有已知得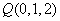 ,
,
得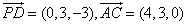 .
.
设平面QAC的法向量为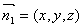 ,则
,则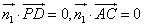 ,
,
即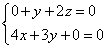 ,∴
,∴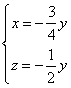 ,
,
令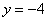 ,得到平面QAC的一个法向量为
,得到平面QAC的一个法向量为
∵PA⊥平面ABCD,∴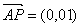 为平面ABCD的法向量.
为平面ABCD的法向量.
设二面角P—CD—B的大小为q,依题意可得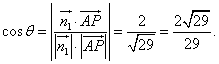 ,
,
(Ⅱ)由(Ⅰ)得
设平面PBD的法向量为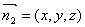 ,则
,则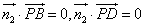 ,
,
即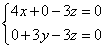 ,∴令
,∴令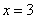 ,得到平面QAC的一个为法向量为
,得到平面QAC的一个为法向量为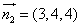
∵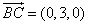 ,
,
∴C到面PBD的距离为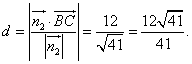

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的解集为
的解集为 ,点
,点 在直线
在直线 上,其中
上,其中 ,则
,则 的最小值为
的最小值为 (B)8 (C)9 (D) 12
(B)8 (C)9 (D) 12 满足
满足
 ,则
,则 ,则
,则 的值为 ;
的值为 ; 、
、 分别为双曲线
分别为双曲线
 的左焦点、右顶点,点
的左焦点、右顶点,点 满足
满足 ,则双曲线的离心率为 ;
,则双曲线的离心率为 ;  的准线方程是( )
的准线方程是( ) B.
B. C.
C. D.
D.
 -
- =1的焦点到渐近线的距离为( )
=1的焦点到渐近线的距离为( ) B.2 C.
B.2 C. D.1
D.1 的中心,则直线EF与面ABC所成的角的大小为
的中心,则直线EF与面ABC所成的角的大小为 B
B C
C D
D
 ,在该几何体的正视图中,这条棱的投影是长为
,在该几何体的正视图中,这条棱的投影是长为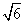 的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为__________
的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为__________