题目内容
已知F(c,0)是椭圆C:
+
=1(a>b>0)的右焦点,圆F:(x-c)2+y2=a2与x轴交于E,D两点,B是椭圆C与圆F的一个交点,且|BD|=
×|BE|.
(1)求椭圆C的离心率;
(2)过点B与圆F相切的直线l与C的另一交点为A,且△ABD的面积等于24×
×
,求椭圆C的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(1)求椭圆C的离心率;
(2)过点B与圆F相切的直线l与C的另一交点为A,且△ABD的面积等于24×
| 6 |
| c |
| 13 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题设条件推导出△BED是直角三角形,△BEF是等边三角形,由此能求出椭圆C的离心率.
(2)由切线性质推导出BF⊥BG,在Rt△BFG中,∠3=30°,直线BG为:y=
x+
c,从而得到yA=
c,OD=OG=3c,GD=6c,由此能求出椭圆C的方程.
(2)由切线性质推导出BF⊥BG,在Rt△BFG中,∠3=30°,直线BG为:y=
| ||
| 3 |
| 3 |
5
| ||
| 13 |
解答:
解:(1)如图,∵EF=BF=DF=a,|BD|=
×|BE|,
∴△BED是直角三角形,∠1=60°,
∵BF=EF,∴△BEF是等边三角形,
∴BF=2OF,
∵OF=c,BF=a,
∴e=
=
.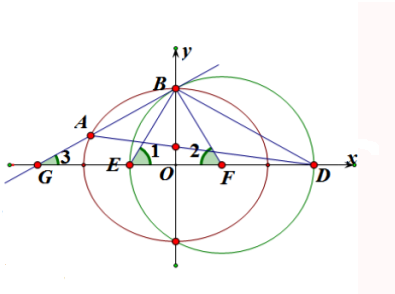
(2)∵过点B与圆F相切的直线l与C的另一交点为A,
∴BF⊥BG,∴在Rt△BFG中,∠3=30°,
∵B(0,
),kBG=
,∴直线BG为:y=
x+
c,
∴
,
解得yA=
c,
∵FD=a=2c,∴OD=OG=3c,∴GD=6c,
∵S△ABD=S△BDG-S△ADG,
c=
GD(BO-yA)=
×6c(
c-
c),
∴c=
,∴a2=8,b2=6,
∴椭圆C的方程为:
+
=1.
| 3 |
∴△BED是直角三角形,∠1=60°,
∵BF=EF,∴△BEF是等边三角形,
∴BF=2OF,
∵OF=c,BF=a,
∴e=
| c |
| a |
| 1 |
| 2 |

(2)∵过点B与圆F相切的直线l与C的另一交点为A,
∴BF⊥BG,∴在Rt△BFG中,∠3=30°,
∵B(0,
| 3c |
| ||
| 3 |
| ||
| 3 |
| 3 |
∴
|
解得yA=
5
| ||
| 13 |
∵FD=a=2c,∴OD=OG=3c,∴GD=6c,
∵S△ABD=S△BDG-S△ADG,
24
| ||
| 13 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
5
| ||
| 13 |
∴c=
| 2 |
∴椭圆C的方程为:
| x2 |
| 8 |
| y2 |
| 6 |
点评:本题考查椭圆的离心率和椭圆方程的求法,是中档题,解题时要注意圆的性质和数形结合思想的灵活运用.

练习册系列答案
相关题目
已知实数x,y满足
,若z=ax+y的最大值为3a+9,最小值为3a-3,则实数a的取值范围为( )
|
| A、[-1,1] |
| B、[-1,2] |
| C、[2,3] |
| D、[-1,3] |
已知集合A={x|x2-3x<0},B={x||x-2|<1},则“a∈A”是“a∈B”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
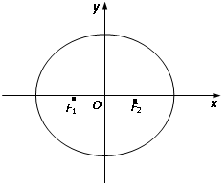 如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-
如图所示,已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),且F2到直线x-