题目内容
从0~9这10个数中,选出3个数作为函数f(x)=ax2+bx+c各项系数,则可以组成不同的二次函数( )个.
| A、900 | B、1000 |
| C、648 | D、720 |
考点:计数原理的应用
专题:应用题,排列组合
分析:由题意,a有9种取法,b,c有10种取法,根据乘法原理,可得结论.
解答:
解:由题意,a有9种取法,b,c有10种取法,
根据乘法原理,可得组成不同的二次函数有9×10×10=900个,
故选:A
根据乘法原理,可得组成不同的二次函数有9×10×10=900个,
故选:A
点评:本题考查计数原理的应用,考查学生的计算能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知{an}是等差数列,a1+a2=4,a7+a8=28,则该数列前8项和S8等于( )
| A、72 | B、64 |
| C、100 | D、120 |
| sin2600° |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、
|
 如图,已知平行四边形ABCD中,E、F分别为边AB、AD上的点,EF与对角线AC交于点P.若
如图,已知平行四边形ABCD中,E、F分别为边AB、AD上的点,EF与对角线AC交于点P.若| AE |
| EB |
| a |
| b |
| AF |
| FD |
| m |
| n |
| AP |
| PC |
A、
| ||
B、
| ||
C、
| ||
D、
|
数列{an}满足:a1a2a3…an=
,则a2013=( )
| 1 |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
若n为奇数,8n-Cn18n-1+Cn28n-2-…+Cnn-18被6除所得的余数是( )
| A、0 | B、1 | C、2 | D、3 |
已知实数a,b满足a2+b2=1,则a4+ab+b4的最小值为( )
A、-
| ||
| B、0 | ||
| C、1 | ||
D、
|
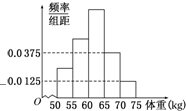 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数为( )
如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数为( )