题目内容
若对任意x∈A,y∈B,(A⊆R,B⊆R)有唯一确定的f(x ,y)与之对应,则称f(x,y)为关于x,y的二元函数.满足下列性质的二元函数
,y)与之对应,则称f(x,y)为关于x,y的二元函数.满足下列性质的二元函数 f(x,y)称为关于实数x,y的广义“距离”:
f(x,y)称为关于实数x,y的广义“距离”:
(1)非负性:f(x,y)≥0,当且仅当x=y时取等号;
(2)对称性:f(x,y)=f(y,x);
(3)三角形不等式:f(x,y)≤f(x,z)+f(z,y)对任意的实数z均成立.
今给出三个二元函数:①f(x,y)=|x-y|;②f(x,y)=(x-y)2;③f(x,y)=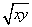 .
.
其中能够成为关于x,y的广义“距离”的二元函数的序号是( )
A.① B.①② C.②③ D.①②③
A
解析:对函数f(x,y)=|x-y|,∵f(x,y)≥0,当且仅当x=y时取等号,满足非负性;
f(y,x)=|y-x|=|x-y|=f(x,y),满足对称性;
由|a+b|≤|a|+|b|得|x-y|=|(x-z)+(z-y)|≤|x-z| +|z-y|对任意的实数z均成立.
+|z-y|对任意的实数z均成立.
即f(x,y)≤f(x,z)+f(z,y),满足三角形不等式.故①满足广义“距离”.
对函数f(x,y)=(x-y)2,显然满足非负性和对称性.
∵当z=0时,f(x,y)-[f(x,0)+f(0,y)]=-2xy,显然不恒小于等于零,故不满足三角形不等式,故②不满足广义“距离”.
对函数f(x,y)=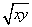 ,显然不满足对称性.故③不满足广义“距离”.故选A.
,显然不满足对称性.故③不满足广义“距离”.故选A.

练习册系列答案
相关题目
 医疗队,如果要求内科医生和外科医生中都有人参加,则有 种选法(用数字作答).
医疗队,如果要求内科医生和外科医生中都有人参加,则有 种选法(用数字作答). ,则
,则 .
. 的解集为
的解集为 ,则实数k=__________.
,则实数k=__________.  、
、 、
、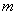 满足
满足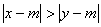 ,则称
,则称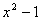 比
比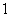 远离0,求
远离0,求 (2)对于任意两个不相等的正数
(2)对于任意两个不相等的正数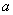 、
、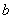 ,证明:
,证明: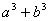 比
比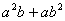 远离
远离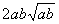 ;
;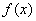 的定义域
的定义域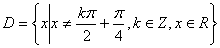 . 任取
. 任取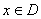 ,
,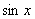 和
和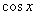 中远离0的那个值,写出函数
中远离0的那个值,写出函数 是由正数组成的等比数列,
是由正数组成的等比数列,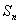 表示数列
表示数列 项的和,
项的和, 若
若 ,
, ,则
,则 的值为( )
的值为( ) B.69 C.93 D.189
B.69 C.93 D.189 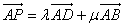 (λ,μ∈R),则λ+μ的取值范围是( )
(λ,μ∈R),则λ+μ的取值范围是( )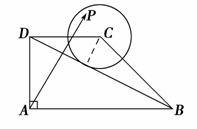
 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 ,
, ,
, 的值;
的值; 的值.
的值.