题目内容
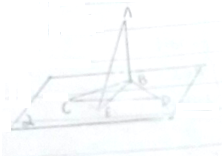 如图,AB=5cm,BC⊥AB,BD⊥AB,在BC,BD所在的平面α内任取一点E,BE=7cm.
如图,AB=5cm,BC⊥AB,BD⊥AB,在BC,BD所在的平面α内任取一点E,BE=7cm.(1)EB和AB,CD和AB成多少度角?
(2)AE的长是多少?
考点:异面直线及其所成的角,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(1)根据BC⊥AB,BD⊥AB,证明AB⊥平面α,从而得出AB⊥BE,AB⊥CD,即EB和AB以及CD和AB所成的角;
(2)在△ABE中,由勾股定理求出AE的值.
(2)在△ABE中,由勾股定理求出AE的值.
解答:
解:(1)∵BC⊥AB,BD⊥AB,
BC?α,BD?α,且BC∩BD=B,
∴AB⊥α;
又∵BE?α,CD?α,
∴AB⊥BE,AB⊥CD;
∴EB和AB成90°角,CD和AB成90°角;
(2)△ABE中,∵AB⊥BE,AB=5cm,BE=7cm,
∴AE=
=
cm.
BC?α,BD?α,且BC∩BD=B,
∴AB⊥α;
又∵BE?α,CD?α,
∴AB⊥BE,AB⊥CD;
∴EB和AB成90°角,CD和AB成90°角;
(2)△ABE中,∵AB⊥BE,AB=5cm,BE=7cm,
∴AE=
| 52+72 |
| 74 |
点评:本题考查了空间中的垂直关系的应用问题,也考查了勾股定理的应用问题,是基础题目.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知复数z=(-8-7i)(-3i),则z在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知数列{an}的通项公式是an=
(n∈N*),若an+an+1=
-3,则n的值是( )
| 1 | ||||
|
| 11 |
| A、10 | B、9 | C、8 | D、6 |