题目内容
若函数f(n)=k,其中n∈N,k是e=2.718281828459…的小数点后的第n位数字,例如f(3)=8,则f{f…f[f(4)]}(共2012个f)= .
考点:函数的值
专题:函数的性质及应用
分析:先由题设条件,得出f(4)=2,f(f(4))=1,…,f(f(f(f(f(f(f(4)))))))=f(7)=8,往后出现循环,因此推导出f{f…f[f(4)]}(共2012个f)问题得到解决.
解答:
解:由题设条件,得出f(4)=2
∴f(f(4))=f(2)=1,
∴f(f(f(4)))=f(1)=7,
∴f(f(f(f(4))))=f(7)=8,
∴f(f(f(f(f(4)))))=f(8)=2,
∴f(f(f(f(f(4)))))=f(f(2))=1,
往后出现循环,4为周期,
因此推导出f{f…f[f(4)]}(共2012个f)=f(f(f(f(4))))=f(7)=8.
故答案为:8.
∴f(f(4))=f(2)=1,
∴f(f(f(4)))=f(1)=7,
∴f(f(f(f(4))))=f(7)=8,
∴f(f(f(f(f(4)))))=f(8)=2,
∴f(f(f(f(f(4)))))=f(f(2))=1,
往后出现循环,4为周期,
因此推导出f{f…f[f(4)]}(共2012个f)=f(f(f(f(4))))=f(7)=8.
故答案为:8.
点评:本题考查函数值的求法,和函数的周期性,属于基础题.解题时要结合题设条件,注意公式的合理选用,耐心地进行计算,总可以得出函数的最终值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,A=
,B=
,a=10,则b=( )
| π |
| 4 |
| π |
| 6 |
A、5
| ||
B、10
| ||
C、10
| ||
D、5
|
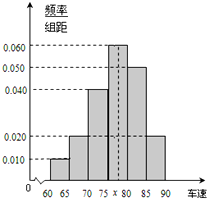 2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.若从车速在[60,70)的车辆中任抽取2辆,则车速在[65,70)的车辆至少有一辆的概率
2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.若从车速在[60,70)的车辆中任抽取2辆,则车速在[65,70)的车辆至少有一辆的概率