题目内容
已知集合A={(x,y)|(x-2)2+(y-3)2=1},B={(x,y)||x-2|+|y-3|=m},若A∩B≠∅,则实数m的取值范围是 .
考点:直线与圆的位置关系,集合的包含关系判断及应用
专题:集合
分析:集合A表示一个以C(2,3)为圆心、半径等于1的圆.而B表示以(2,3)为中心的一个正方形,求得其中一个边所在的直线方程为x+y-5-m=0.由A∩B≠∅,则圆心到正方形的边的距离大于或等于
且小于或等于半径1,由此求得m的范围.
| ||
| 2 |
解答:
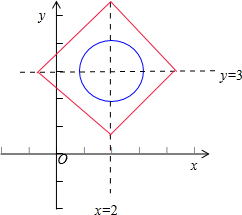 解:集合A={(x,y)|(x-2)2+(y-3)2=1},
解:集合A={(x,y)|(x-2)2+(y-3)2=1},
表示一个以C(2,3)为圆心、半径等于1的圆.
而B={(x,y)||x-2|+|y-3|=m},表示以(2,3)为
中心的一个正方形,
其中一个边所在的直线方程为x+y-5-m=0.
当正方形的四个顶点在圆上时,
圆心到正方形的边的距离等于
,
当圆和正方形相切时,圆心到正方形的边的距离等于半径1,
故由 A∩B≠∅,则圆心到正方形的边的距离
大于或等于
且小于或等于半径1,
即
≤
≤1,即 1≤|m+1|≤
,
即 1≤m+1≤
,或-
≤m+1≤-1,
解得 0≤m≤
-1,或-1-
≤m≤-2,
故答案为:{m|-1-
≤m≤-2,或0≤m≤
-1 }.
 解:集合A={(x,y)|(x-2)2+(y-3)2=1},
解:集合A={(x,y)|(x-2)2+(y-3)2=1},表示一个以C(2,3)为圆心、半径等于1的圆.
而B={(x,y)||x-2|+|y-3|=m},表示以(2,3)为
中心的一个正方形,
其中一个边所在的直线方程为x+y-5-m=0.
当正方形的四个顶点在圆上时,
圆心到正方形的边的距离等于
| ||
| 2 |
当圆和正方形相切时,圆心到正方形的边的距离等于半径1,
故由 A∩B≠∅,则圆心到正方形的边的距离
大于或等于
| ||
| 2 |
即
| ||
| 2 |
| |2+3-5-m| | ||
|
| 2 |
即 1≤m+1≤
| 2 |
| 2 |
解得 0≤m≤
| 2 |
| 2 |
故答案为:{m|-1-
| 2 |
| 2 |
点评:本题重点考查了集合的交集运算、圆与直线的位置关系判断等方法,属于中档题.

练习册系列答案
相关题目
 某数学爱好者设计了一个食品商标,如果在该商标所在平面内建立如图所示的平面直角坐标系xOy,则商标的边缘轮廓线AOC恰是函数y=tan
某数学爱好者设计了一个食品商标,如果在该商标所在平面内建立如图所示的平面直角坐标系xOy,则商标的边缘轮廓线AOC恰是函数y=tan